Нужно найти sin x, если cos x = 8/17; 3/2пи меньше x меньше 2 пи. и, если можно, объясните, как определить, в какой четверти находится значение, и как оно влияет на ответ.
Другие вопросы по теме Математика
Популярные вопросы
- Бабочка вылетает по направлению с запада на восток в абсолютно безветренную...
3 - Что включает в себя национальные интересы России...
2 - Сумативи ова е за раз «Путешеrаѕѕ в з Вы речевой деятельности Сушене а...
3 - Котре з дієслів не на належать до першої дієособи а) малювати б) брати...
3 - завдання 10 слів з Орфограмою і скласти 1 речення...
3 - Эркин, Акмал, Сардор, Бобур и Шерзод решили купить яблоки. Оказалось что...
3 - Решите задачу. Впишите результаты промежуточных вычислений и ответ. К 150...
3 - Чому правдоборець Чіпка став вбивцею?...
3 - Сократите дробь 24/56 до несократимой...
2 - На відрізку AB довжиною 36см взято точку С. Знайдіть довжини відрізків...
1
Согласно условию, значение Х находится в 4-й четверти. Синус в четвёртой степени ОТРИЦАТЕЛЕН. Следовательно,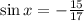
Четверти всего четыре -![\left[0;\frac{\pi}2\right],\quad\left[\frac{\pi}2;\pi\right],\quad\left[\pi;\frac{3\pi}2\right],\quad\left[\frac{3\pi}2\right,2\pi]](/tpl/images/0117/3099/90e9b.png)
Влияет на ответ так: синус положителен в 1й и 2й четвертях, отрцателен в 3й и 4й; косинус положителен в 1й и 4й четвертях, отрицателен во 2й и 3й.