Нужно найти предел функции под буквой f. кто разбирается,
Другие вопросы по теме Математика
Популярные вопросы
- , сделать номер 1(б, в) Номер 2...
2 - Зачеркните в каждом ряду лишнее слово. Расписка, инструкция,...
3 - Масштаб виду в «1 см – 500 км» називається А) Числовим Б) Іменним...
1 - 4. Если двузначное число разделить на число, записанное теми...
1 - Токырау жылдарынлагы казакстандагы онеркасип дамуы жагдайы...
2 - Дано вершини трикутника М(-2;3)N(1;6)E(2;-1) Знайдіть косинуси...
1 - 4. На рисунке ZB =2C = 750, L.BAO =Z.CDO = 25°. Найдите значение...
3 - надо решить как задачку с дано и решением с 9 по...
1 - Чесе е Задания суммативного оценивания за 2 четверть 1. Сравните...
3 - Көтерілген мәселелер?Негізгі ойы?...
2
Бесконечно малые функции: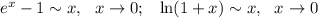 . Используем формулу сокращенного умножения:
. Используем формулу сокращенного умножения:
Для n = 7 мы имеем
Положим![a=\sqrt[7]{1+3x}](/tpl/images/1047/0962/df52a.png) и
и 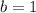 , тогда
, тогда
Подставив x = 0 в числителе третьего множителя, мы найдем значение