Нужно найти обший вид числовое последовательности: 2; 2½; 2⅓; 2¼.
Другие вопросы по теме Математика
Популярные вопросы
- Первая междоусобица на руси возникла: 1 после гибели святослава...
2 - нужно написать по сочинение моя любимая книга...
3 - Как протекает диффузия в жидкостях ? опишите опыт ....
3 - Врезультати разлома гондвали возникли...
3 - Уроки в школе начинаются в 9 00.во сколько надо встать если сборы...
1 - Через точку а (-7; 5) проведена прямая,параллельная оси ординат.какая...
1 - Каким образовано слово сжатый ?...
1 - 1)длина диагонали куба 4корень из 3 см. найдите ребро куба...
2 - Сколько шестых долей содержится в 1/2, 1/3, 2/3, 3/2....
1 - Какие события и люди были в центре изображения произведений...
2
2; 2½; 2⅓; 2¼... - числовая последовательность, начиная со второго члена, монотонно убывающая.
Проверка :
n = 1;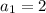
n = 2;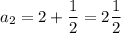
n = 3;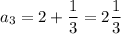
n = 4;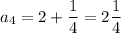
===============================================
[(n-1):n] - математическое округление "до целого". Результат деления (n-1):n будет равен 0 при n=1, и будет округляться к 1 при любых n>1.
Проверка:
n = 1;![a_1=2+\dfrac{[(1-1):1]}1=2+\dfrac{0}1=2](/tpl/images/0967/0418/c501a.png)
n = 2;![a_2=2+\dfrac{[(2-1):2]}2=2+\dfrac{[0,5]}2=2+\dfrac{1}2=2\dfrac{1}2](/tpl/images/0967/0418/f3a63.png)
n = 3;![a_3=2+\dfrac{[(3-1):3]}3=2+\dfrac{[0,(6)]}3=2+\dfrac{1}3=2\dfrac{1}3](/tpl/images/0967/0418/9224d.png)
n = 4;![a_4=2+\dfrac{[(4-1):4]}4=2+\dfrac{[0,75]}4=2+\dfrac{1}4=2\dfrac{1}4](/tpl/images/0967/0418/d55f3.png)