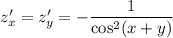Нужно найти частные производные функции z=ctg(x+y). Не очень понимаю, как делать
Другие вопросы по теме Математика
Популярные вопросы
- Вызначце, якім шляхам утвораны словы і ад якіх: Высока-навекі-назаўсёды-двойчы-па-мойму-моўчкі-навостраны-пакруціўшы-...
1 - 1. Определить слово по его лексическому значению. 1) Речь одного человека, обращенная...
2 - Травна система безхребетних тварин 1. Травний канал яких тварин має найпримітивнішу...
3 - В одной координатной плоскости построить фотку как это сделать...
2 - Дано натуральное число. Напишите программу, которая вычисляет сколько раз в нем...
3 - 2(2-y)=y-5решите действия полностью...
3 - Придумать видео ролик,рекламы сказки Снегурочка .....
2 - мәтіннен құрмалас сөйлемдерді теріп жазып олардың жасалу жолын түрін ажыратыңдар.салалас...
1 - Які існують закономірності зміни ґрунтів на рівнинах і в горах? Якими чинниками...
3 - Определите значение слов запишите в тетрадь: помещик, мировой судья, окружной...
1
Если существует предел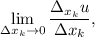 то этот предел называется частной производной от функции
то этот предел называется частной производной от функции 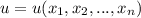 по переменной
по переменной 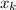 и обозначается
и обозначается 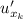 или
или 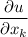
Для функции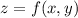 следует найти частные производные
следует найти частные производные 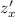 и
и 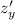
Для нахождения таких производных по данной переменной следует все переменные, кроме данной, считать константами (числами).
Например, для функции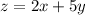 частной производной функции по переменной
частной производной функции по переменной  будет:
будет: 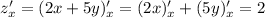 (считаем выражение
(считаем выражение 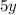 числовым, производная от которого равна нулю), и аналогично по переменной
числовым, производная от которого равна нулю), и аналогично по переменной 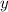 будет:
будет: 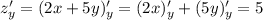
Для заданной функции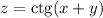 найдем частные производные
найдем частные производные 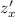 и
и 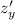
Воспользуемся формулой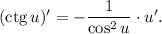
Имеем:
ответ: