Нужно доказать параллельность прямых
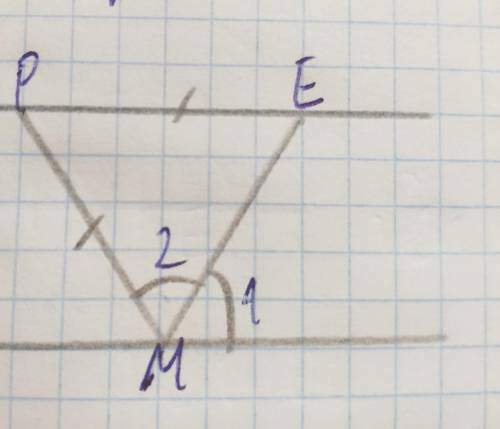
Другие вопросы по теме Математика
Популярные вопросы
- Впрямоугольнике одна сторона равна 28 см, а диагональ равна 35...
3 - Улюдини кучеряве волосся є домінантною ознакою, пряме волосся-...
2 - Sin^2x+cos^2x-1 найти значения выражения...
2 - Гетерозиготний чоловік з темною емаллю зубів домінантна ознака...
3 - Яке значення для західноукраїнських земель мала весна народів...
1 - Движение материальной точки описывается уравнением x=25-10t+2t^2.считая...
3 - )мне для читательского дневника нужно краткое содержание книги...
3 - Из полного бокала, имеющего форму конуса высотой 9 , отлили треть...
1 - (нужно краткое содержание книги ромео и джульетта.совсем краткое,для...
3 - Отношение скорости света в вакууме к скорости света в среде называется...
3
прямые параллельны по 2 му признаку - равенству накрест лежащих углов ∠РЕМ = ∠1
Пошаговое объяснение:
2й признак параллельности прямых гласит
Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180° — то прямые параллельны.
в нашем случае докажем, что накрест лежащие углы равны.
у нас накрест лежащие углы это ∠РЕМ и ∠1. докажем их равенство
РМ =РЕ , значит ΔРМЕ - равнобедренный, а значит ∠РЕМ = РМЕ
а поскольку по условию ∠РМЕ (∠2) =∠1, то ∠РЕМ = ∠1
что и требовалось доказать
Одним из таких свойств является угол между параллельными прямыми и пересекающей их прямой. Углы, образованные пересекающей прямой и параллельными прямыми, будут равны между собой.
В данной задаче нам дана прямая a и две прямые b и c. Нам нужно доказать, что прямые b и c параллельны.
Давайте рассмотрим углы, сформированные прямыми a, b и c. Обозначим их как углы α и β.
Угол α образован пересекающей прямой a и прямой b, а угол β образован пересекающей прямой a и прямой c.
Нам нужно доказать, что углы α и β равны, чтобы доказать параллельность прямых b и c.
По условию, у нас дано, что угол α = 60°.
Теперь давайте рассмотрим угол β. В треугольнике ABC в равнобедренном треугольнике ACB (который прямой), у нас два одинаковых угла в вершинах A (угол β) и C (угол α).
Таким образом, мы можем утверждать, что угол β также равен 60°.
Следовательно, угол α = 60° и угол β = 60°, что означает, что углы, образованные прямыми a, b и c, равны между собой.
Таким образом, прямые b и c параллельны между собой, потому что углы, образованные ими и пересекающей прямой a, равны между собой.
Итак, мы доказали параллельность прямых b и c, используя свойство равенства углов, образованных пересекающей прямой и параллельными прямыми.