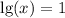нужна желательно решение на бумаге. Могу закрыть вопрос за подсказку, которую я посчитаю весомой.
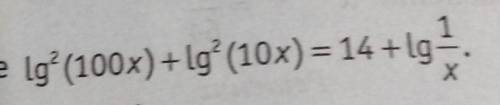
Другие вопросы по теме Математика
Популярные вопросы
- Запиши в виде десятичной дроби: 14 целых 2/5...
3 - вот так напишите А Б В Г вот так напишите А Б В Г >...
1 - Найдите значение выражения Там где 4 находится 10, а там где 2 11...
2 - Найти ошибки в 3 предложениях. [ ] - там ошибка 1)My son saw a car which(здесь...
1 - Время глагола замёрз, ушибся, ...
1 - Відомі вірші М.Рильського...
2 - Укажіть фермент слини? А)пепсик Б)муцик В)мізоцим Г)тримпсик...
1 - Кількість пасажирних місць у спальному, купейному та плацкартному вагонах...
3 - Какое общественное здоровье обличает Маяковский в произведении Мама и убитый...
1 - 1. Вычислите: 12^1∕ 3∙ 6^2∕ 3· (0,5^)1∕ 3=-5/132. Найдите sin x, если cos...
3
ОДЗ: x > 0.
1.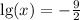
2.