Нужна ! макс ! решить диф уравнения (y"')^2+(y")^2=0 - надо

Сумма двух квадратов равна нулю тогда и только тогда, когда оба равны нулю:

Но из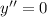 следует, что 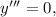поэтому остается решить уравнение 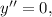то есть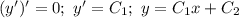

ответ: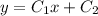

Это дифференциальное уравнение второй степени, не содержащее явно х, третьего порядка. Квадраты производных второго и третьего порядков равны нулю, т.к. сумма квадратов равна нулю только в случае равенства нулю каждого слагаемого. Но если игрек два штриха равно нулю. то производная нуля тоже равна нулю. и тогда производная и третьего порядка равна нулю. значит,  решив уравнение игрек два штриха равно нулю, мы получим решение исходного уравнения. вторая производная - это первая производная от первой производной. Поэтому производная от (у штрих ) =0, когда у штрих равен константе, например, с₁, а, значит,

у = с₁х+с₂, где с₁ и с₂ - произвольные постоянные и есть решением исходного уравнения.