нужна , исследовать степенной ряд схождения!
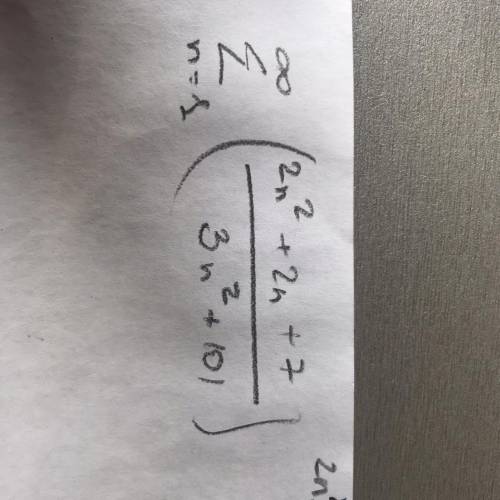
Другие вопросы по теме Математика
Популярные вопросы
- Закончите вопросы: The little plump woman standing at the window is my...
1 - Когда мы переводим предложение в времени из прямой речи в косвенную, все...
2 - Дайте перевод слова на английский язык: крестный Godfather...
2 - Закончите вопросы: He didn t lose the keys_? did he hasn’t she did we...
2 - Выберите подходящую форму причастия: I will show you a picture _ by Helen...
1 - Translate: accountant бухгалтер повар политик рассказчик...
2 - Выберите подходящую форму причастия: _ to the theatre, she saw that the...
2 - In the north of Europe the climate has become milder and warmer too, _?...
2 - Вставьте пропущенное слово: The National Curriculum _ not apply in Scotland,...
2 - The British people elect 650 members of the House of Commons every five...
2
Применим радикальный признак Коши.
Ряд сходится, так как получили число, меньшее 1 .