1. Математика
  2. Нужна 10 класс тригонометрия

Нужна
10 класс тригонометрия формулы произведений синусов косинусов и тому подобное

Женечка180510 Женечка180510    2   18.11.2019 14:15    1

Ответы
6561813 6561813  10.10.2020 13:59

x=\pm\frac{\pi}{8}+\frac{\pi n}{2},n\in Z

Пошаговое объяснение:

2cos^62x-cos^42x+1.5sin^24x-3sin^22x=0

Перейдем к аргументу 4x.

1)cos^62x=(cos^22x)^3=(\frac{1}{2}(2cos^22x-1)+\frac{1}{2})^3=(\frac{1}{2}(cos4x+1))^3,\\2)cos^42x=(cos^22x)^2=(\frac{1}{2}(2cos^22x-1)+\frac{1}{2})^2=(\frac{1}{2}(cos4x+1))^2\\3)sin^24x=1-cos^24x\\4)sin^22x=-\frac{1}{2}(1-2sin^22x)+\frac{1}{2}=-\frac{1}{2}cos4x+\frac{1}{2}

Преобразуем уравнение:

2(\frac{1}{2}(cos4x+1))^3-(\frac{1}{2}(cos4x+1))^2+\frac{3}{2}(1-cos^24x)-3(-\frac{1}{2}cos4x+\frac{1}{2})=0,\\(cos4x+1)^3-(cos4x+1)^2-6cos^24x+6cos4x=0\\(cos4x+1)^2(cos4x+1-1)-6cos^24x+6cos4x=0\\cos4x((cos4x+1)^2-6cos4x+6)=0\\cos4x(cos^24x-4cos4x+7)=0

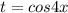Пусть t=cos4x. Получим два уравнения:

t=0,\\t^2-4t+7=0

Во втором уравнении:

D=(-4)^2-4*7=-12 - действительных решений нет.

Вернемся к исходной переменной.

cos4x=0,\\4x=\pm\frac{\pi}{2}+2\pi n,\\x=\pm\frac{\pi}{8}+\frac{\pi n}{2},n\in Z

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
vadimmka666 vadimmka666  08.09.2019 04:20
Запиши дробь 2/9 в виде дроби со знаменателем 45....
Katyamaier777 Katyamaier777  08.09.2019 04:20
При яких значення змінної має зміст вираз: 8 х-4...
Соломія2203 Соломія2203  08.09.2019 04:20
Сколько будет 2 кг 600 г , если перевести в граммы ?...
рогозина рогозина  08.09.2019 04:20
Запиши дробь 2/9 в виде дроби со знаменателем 45....
Заразный1 Заразный1  08.09.2019 04:20
70-(81-39): 7+6х7= решить по действиям...
MariCasanova MariCasanova  08.09.2019 04:20
В5 одинаковых в банках 50 литров сока. сколько литров в 9 таких банках? уровень сложности: eazy...
snady snady  08.09.2019 04:20
F(x)=9x^8+2x+cos x найти первообразную...
Александра2280193 Александра2280193  08.09.2019 04:20
Длина посадочной дороги 7 км а длина шоссе 63 км на сколько километров просёлак короче шоссе? во сколько раз шоссе длиннее просёлка? заранее!...
ApostalVooDoo ApostalVooDoo  08.09.2019 04:20
Найдите значение выражения (для тех α, при которых выражение определено ) 6sin(α−π)\(2cos(π/2+α)−cos(3π/2+α))...
gagikgrigoryan gagikgrigoryan  08.09.2019 04:20
Реши уравнения с объяснением: 1) (39+х)-84=78 2) (х-83)=316=425 3) (600-х)-92=126...

Популярные вопросы