Нужен ответ с об'яснением
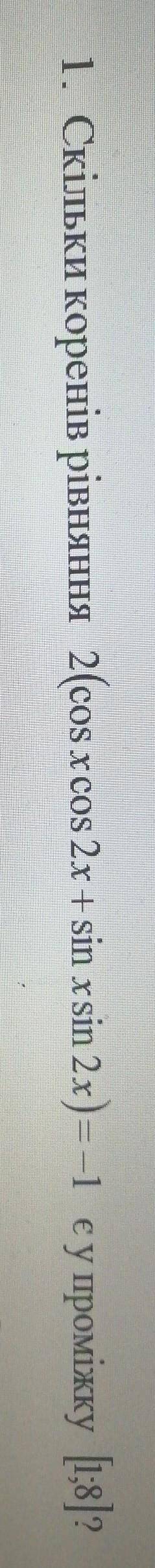
Другие вопросы по теме Математика
Популярные вопросы
- Выпишите из произведения ,,размышление у парадного подъезда н.некрасов...
2 - Разделите 4 евро на две части так,что бы обна часть была в 4 раза...
2 - Перевести в кубические сантиметры 6000 мм2; 13дм3 7см3....
1 - Краткое содержание произведения муму ( примерно 1 абзац,ну чуть чуть...
1 - Ни остне и на березе бахрома белой пряжей их запутала зима . и не...
1 - Может ли современный школьник обойтись без интернета рассуждение...
3 - Какие города казахстана стоят на реке урал? а) орск, магнитагорск...
1 - Сколько миллилитров составляет 2/5 я часть 3/8л...
2 - Составить предложения употребив их в различных падежах. родной (...
2 - Глубина лужи 8 см определите давление воды на дно лужи...
1
по формуле косинуса разности имеем
cos(x-y) ≡ cos(x)·cos(y) + sin(x)·sin(y)
поэтому
cos(x)·cos(2x) + sin(x)·sin(2x) ≡ cos(2x - x) ≡ cos(x),
Поэтому исходное уравнение равносильно
2·cos(x) = -1,
cos(x) = -1/2,
решаем это элементарное тригонометрическое уравнение,
x = ±arccos(-1/2) + 2πm, m∈Z
x = ±(π - (π/3)) + 2πm
x = ±(2π/3) + 2πm
Имеем две серии решений:
x₁ = (2π/3) + 2πm₁, m₁∈Z
x₂ = -(2π/3) + 2πm₂, m₂∈Z,
Проверим, какие из решений удовлетворяют условию 1≤x≤8.
Т.к. 3,14 < π < 3,15, то имеем
1) 2π/3 > π/2 > 1, и
(2π/3) + 2π > 8, ⇔ 8π/3 > 8, ⇔ π/3 > 1, ⇔ π > 3.
поэтому очевидно, что первая серия решений дает лишь одно значение на отрезке [1; 8], и это значение 2π/3
2) 2π - (2π/3) > 1, ⇔ 4π/3 > 1, ⇔ π > 3/4 , очевидно верно,
2π - (2π/3) < 8, ⇔ 4π/3 < 8, ⇔ π < 6, очевидно верно,
4π - (2π/3) > 8, ⇔ 10π/3 > 8, ⇔ π > 12/5 = 2+ (2/5) очевидно верно.
вторая серия решений дает лишь одно значение на отрезке [1;8], это значение есть (2π - (2π/3)) = 4π/3.
Итак, всего два решения на отрезке [1;8].