Номер 836 . Дайте полный ответ в тетради
2) ||3x-2|+3|=7
3) ||4x+3|-5|=8
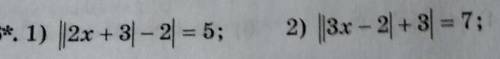
Другие вопросы по теме Математика
Популярные вопросы
- Укажите факторы оказавшие влияние на социальное положение народа в военные...
1 - СОЧ по английскому (у меня 2 часа до уроков ...
1 - , заполнить таблицу И БЫСТРО...
3 - ЗАДАНИЕ №2 ОБЩЕЕ ВРЕМЯ: 36:49ВРЕМЯ НА ЗАДАНИЕ: 00:15ТЕКСТ ЗАДАНИЯОқылымМәтінді...
2 - В кинотеатре n рядов кресел. В первом ряду k кресел, в каждом последующем...
3 - ребята у меня такая проблема когда прихожу в школу меня высерают что я...
2 - 1. Берілген сөйлемді мағынасын сақтап, өз сөзіңізбен жазыңыз. Жануарлардың...
2 - СОЧ ПО РУССКОМУ ЯЗЫКУ 5 КЛАСС 3 ЧЕТВЕРТЬ Прочитайте текст и ответьте на...
3 - спишите, вставьте пропущенные орфограммы, расставьте недостающие знаки...
1 - «Менің атым Қожа» әңгімесіндегі Қожаның мінезі, оның өмірге деген өзіндік...
3
1)||2x+3|-2|=5 2) ||3x-2|+3|=7 3)||4x+3|-5|=8
[2x+3]-2=5 [3x-2]=3=7 x=5/2
[2x+3]-2=-5 [3x-2]=7-3 х=-4
x=2 [3x-2]=4 x=-4,x=5/2
x=-5 x=-2/3
x=-5,x=2 x=2
x=-2/3,x=2
2) ||3x-2|+3|=7
Чтобы найти решение этого уравнения, нужно рассмотреть два варианта:
a) Если выражение внутри двойной модулировочки является положительным или нулевым, то уравнение примет вид: |3x-2|+3=7.
Вычитаем 3 из обеих частей, получаем: |3x-2|=4.
Так как модуль числа может быть только положительным или нулевым, то имеем два варианта дальнейших действий:
- Если 3x-2 > 0, то модуль просто остается как есть: 3x-2=4. Добавляем 2 к обеим частям, получаем: 3x=6. Делим на 3, получаем: x=2.
- Если 3x-2 < 0, то модуль приобретает знак минус: -(3x-2)=4. Раскрываем скобки и домножаем на -1: -3x+2=4. Вычитаем 2 из обеих частей, получаем: -3x=2. Делим на -3, получаем: x=-2/3.
b) Если выражение внутри двойной модулировочки является отрицательным, то уравнение примет вид: -(3x-2)+3=7.
Раскрываем скобки и прибавляем 3 к обеим частям, получаем: -3x+2+3=7. Вычитаем 5 из обеих частей, получаем: -3x+5=7. Вычитаем 5 из обеих частей, получаем: -3x=2. Делим на -3, получаем: x=-2/3.
Таким образом, решением уравнения будет множество {-2/3, 2}.
3) ||4x+3|-5|=8
Аналогично, разберемся с различными вариантами:
a) Если выражение внутри двойной модулировочки является положительным или нулевым, то уравнение примет вид: |4x+3|-5=8.
Добавим 5 к обеим частям, получаем: |4x+3|=13.
Рассмотрим два варианта дальнейших действий:
- Если 4x+3 > 0, то модуль остается без изменений: 4x+3=13. Вычитаем 3 из обеих частей, получаем: 4x=10. Делим на 4, получаем: x=10/4 = 5/2.
- Если 4x+3 < 0, то модуль приобретает знак минус: -(4x+3)=13. Раскрываем скобки и домножаем на -1: -4x-3=13. Вычитаем 3 из обеих частей, получаем: -4x=16. Делим на -4, получаем: x=-4.
b) Если выражение внутри двойной модулировочки является отрицательным, то уравнение примет вид: -(4x+3)-5=8.
Раскрываем скобки и прибавляем 5 к обеим частям, получаем: -4x-3+5=8. Вычитаем 3 из обеих частей, получаем: -4x+2=8. Вычитаем 2 из обеих частей, получаем: -4x=6. Делим на -4, получаем: x=-6/4 = -3/2.
Таким образом, решением уравнения будет множество {-3/2, -4, 5/2}.