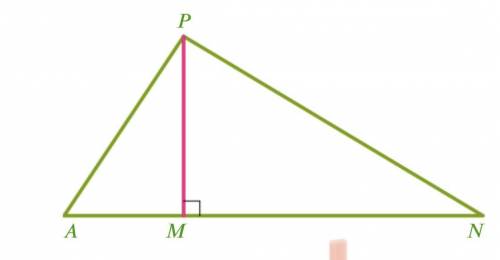
Nogriezni.png Сравни длины отрезков, выходящих из вершины , если ∡=80°, ∡=50°.

Расположи отрезки в порядке возрастания их длин:

Дано: В треугольнике ABC, ∠B = 80° и ∠C = 50°.

Мы должны сравнить длины отрезков, выходящих из вершины B, и разместить их в порядке возрастания.

Чтобы решить эту задачу, мы можем использовать теорему синусов.

Теорема синусов устанавливает соотношение между длинами сторон треугольника и соответствующими им углами.

В нашем случае, мы можем использовать соотношение: \(\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\), где a, b, c - длины сторон треугольника, A, B, C - соответствующие углы.

Мы можем обозначить длины отрезков, выходящих из вершины B, как x и y.

Таким образом, мы получаем следующие уравнения:

\(\frac{x}{\sin(80°)} = \frac{y}{\sin(50°)}\)

Мы можем использовать значение синуса 80° и 50°, которые можно найти в таблице значений тригонометрических функций или с помощью калькулятора.

\(\sin(80°) ≈ 0.9848\)

\(\sin(50°) ≈ 0.7660\)

Подставив эти значения в уравнение, получаем:

\(\frac{x}{0.9848} = \frac{y}{0.7660}\)

Теперь мы можем найти соотношение между x и y:

\(x ≈ 0.9848y\)

Отношение между x и y равно приблизительно 0.9848.

Таким образом, мы можем заключить, что x меньше чем y.

Порядок возрастания длины отрезков будет: x < y.