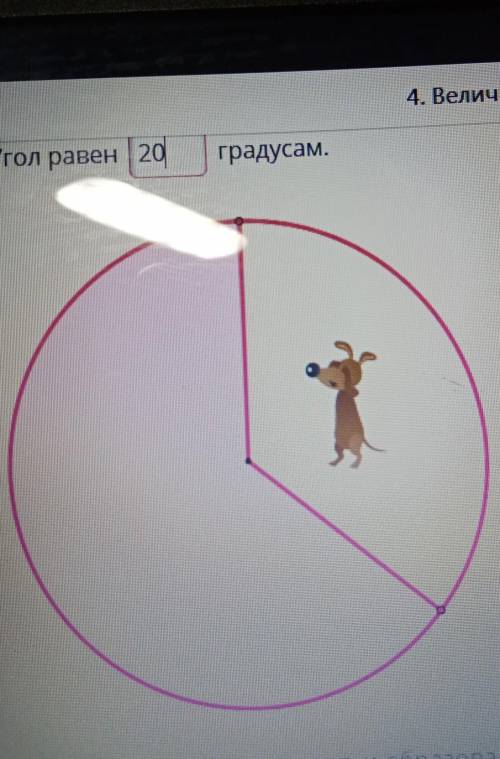
Несколько гостей Взяли торт, и образовался пустой сектор с тупым углом. 2. Определи меньшее число гостей, которые взяли по кусочку торта, если угол сектора уже стал тупым.
Число гостей:
ответить!

3 гостя

Пошаговое объяснение:

а градусы транспортиром померь с экрана

3гостей

Пошаговое объяснение:

Чтобы решить данную задачу, мы должны понять, как формируется сектор с тупым углом в торте.

Давайте разберем изображение торта, чтобы получить как можно более полное представление о ситуации.

На картинке есть круг, который представляет собой весь торт. Также есть два радиуса, один идет от центра к внешнему краю торта (исходный радиус), а другой касается основания сектора (измененный радиус). Оба радиуса делят окружность на две части - большую и меньшую.

На данной картинке изображено, что весь торт был разделен между гостями, и один из гостей взял кусочек торта. При этом образовался пустой сектор с тупым углом (угол между двумя радиусами).

Теперь, чтобы ответить на вопрос "определите меньшее число гостей, которые взяли по кусочку торта, если угол сектора уже стал тупым", мы должны понять, как изменяется угол сектора в зависимости от количества гостей.

Если угол сектора уже является тупым, это означает, что кусочек торта, взятый одним гостем, занимает больше половины всего торта. Таким образом, нам нужно найти количество гостей, которые взяли кусочки торта, превышающие половину общего объема торта.

Давайте предположим, что у нас есть N гостей, которые взяли по кусочку торта. После того, как N-ый гость взял свой кусок, образуется пустой сектор с тупым углом. Изображение показывает, что угол этого сектора образован начальным радиусом и радиусом, продолженным после N-ого гостя (см. картинку).

Угол сектора зависит от площади сектора торта, который взяли гости. Площадь сектора торта можно вычислить по формуле:

S = (угол в радианах / 2π) * π * r^2,

где S - площадь, угол в радианах - угол, образованный радиусами, r - радиус торта.

Если угол сектора является тупым, это означает, что площадь сектора больше половины площади всего торта. То есть:

S > 0.5 * π * r^2.

Если мы заменим S в этом неравенстве на формулу для сектора торта, то получим:

(угол в радианах / 2π) * π * r^2 > 0.5 * π * r^2.

Радиус торта (r^2) сокращается с обеих сторон неравенства:

(угол в радианах / 2π) > 0.5.

Упрощаем уравнение, умножая обе стороны на 2π:

угол в радианах > π.

Таким образом, угол в радианах должен быть больше π (3.14159).

Теперь остается только найти минимальное количество гостей, для которых угол сектора становится больше π (3.14159).

Если мы посмотрим на изображение торта, угол сектора будет увеличиваться с каждым новым гостем. Исходный угол в радианах (размер начального сектора) составляет π (полный сектор). С каждым гостем угол уменьшается. Нам нужно найти номер гостя, при котором угол становится больше π.

Начнем с гостя номер 1. При N = 1, у нас есть только один гость (N = 1), взявший кусочек торта. Угол сектора равен π (поскольку исходный сектор является полным сектором). Таким образом, для гостя номер 1 угол уже больше π.

Идем дальше. Посмотрим на гостя номер 2. При N = 2, у нас есть два гостя, взявших кусочек торта. Угол сектора сократится пополам (поскольку площадь сектора должна быть больше половины площади торта), и будет равен π/2. Этот угол все еще меньше π, поэтому гость номер 2 также удовлетворяет условию.

Мы можем продолжать увеличивать количество гостей и находить угол сектора для каждого из них, пока не найдем минимальное количество гостей, при котором угол становится больше π.

Давайте продолжим, теперь находим угол сектора для гостя номер 3. При N = 3, угол сектора будет равен π/3. Этот угол также меньше π, поэтому гость номер 3 не является ответом.

Мы можем продолжать этот процесс, находить угол сектора для каждого следующего гостя и сравнивать его с π, пока угол не станет больше π.

Давайте проведем еще несколько вычислений:

- Гость номер 4: угол сектора равен π/4. Этот угол все еще меньше π, поэтому гость номер 4 не является ответом.
- Гость номер 5: угол сектора равен π/5. Этот угол все еще меньше π, поэтому гость номер 5 не является ответом.
- Гость номер 6: угол сектора равен π/6. Он больше π! Поэтому минимальное количество гостей, которые должны взять кусочки торта, чтобы угол сектора стал тупым, равно 6.

Итак, ответ на задачу: меньшее число гостей, которые взяли по кусочку торта, при котором угол сектора становится тупым, равно 6.