Неравенство, содержащее А и Р
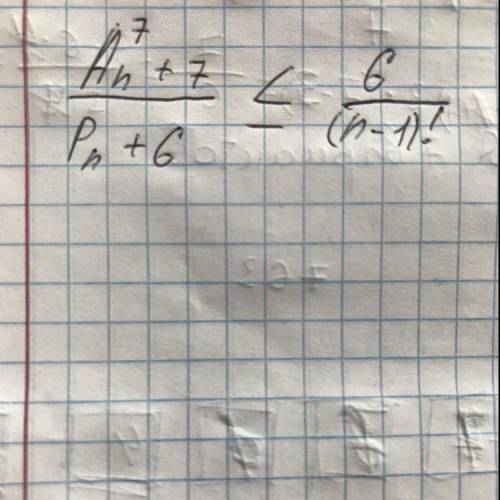
Другие вопросы по теме Математика
Популярные вопросы
- Треугольник авс и рмк равны. известно,что ав=5см,вc=10 см,угол c=36°.найдите...
1 - 73-сабақалматы мен нұр-сұлтанөзің тұратын каланы немесе ауылды өзге жерден...
2 - D. рінверсия2. выделите анафору и инверсию, которые и.а.крылов использует...
2 - 50 за 1 уравнения, 8 класс для аутистов ...
2 - Определите факторы влияющие на исчезновении животных и растений? ...
3 - Очём это произведение и его главная мысль рассказ муму...
2 - Кто решит имено по таблице тому 20 ...
3 - Чему равен модуль числа -2, 3? а)-2,3; в)2,3; с)-13; д)13...
2 - 1. какие виды обшественного транспорта связывают наш город с другими...
3 - Упокрытосеменных растений в результате слияния спермия с центральной...
2
Правила работы с неравенствами:
1. Если неравенство умножается или делится на положительное число, знак неравенства не меняется.
2. Если неравенство умножается или делится на отрицательное число, знак неравенства меняется на противоположный.
3. Если к обеим частям неравенства добавляют или вычитают одно и то же положительное число, знак неравенства не меняется.
4. Если к обеим частям неравенства добавляют или вычитают одно и то же отрицательное число, знак неравенства меняется на противоположный.
Теперь давайте приступим к решению неравенства с помощью этих правил.
Уважаемый школьник, в представленном неравенстве есть две переменные - А и Р. Наша задача заключается в том, чтобы определить диапазон возможных значений переменных А и Р, при которых неравенство будет выполняться.
Давайте рассмотрим неравенство:
А - 3Р < 10
Для начала посмотрим на символ "<" - это означает "меньше". Погодите, давайте изменим направление неравенства, чтобы не было отрицания. Мы можем сделать это, умножив обе части неравенства на -1 и поменяв знак на противоположный:
-1(А - 3Р) > -1(10)
-А + 3Р > -10
Теперь неравенство имеет вид -А + 3Р > -10. Мы применили правило №2 - умножение на отрицательное число, что привело к изменению направления неравенства.
Теперь наша задача состоит в том, чтобы разделить неравенство на 3, чтобы избавиться от коэффициента перед Р:
(-А + 3Р)/3 > -10/3
Мы применили правило №1 - деление на положительное число.
Теперь мы имеем неравенство -А/3 + Р > -10/3.
Наконец, чтобы исключить -А/3, вычтем его из обеих частей неравенства:
(-А/3 -А/3) + Р > -10/3 -А/3
2Р > -10/3 -А/3
Вот и наше решение - неравенство 2Р > -10/3 -А/3. Здесь мы исключили -А/3, вычитая его из обеих частей неравенства.
Наконец, возвращаясь к исходной форме неравенства, заметим, что символ "<" остался без изменений. Что это значит? Это значит, что все значения Р, которые удовлетворяют условию неравенства, находятся справа от линии "<". Объясню это подробнее.
Мы получили 2Р > -10/3 -А/3. Если мы хотим найти диапазон возможных значений Р, то нам нужно отделить переменную Р от остальных членов неравенства, то есть избавиться от -10/3 -А/3.
Если мы сложим -10/3 и 3А/3, получим -10/3 + 3А/3 = (3А - 10)/3.
Итого, неравенство будет иметь вид 2Р > (3А - 10)/3.
Теперь нам нужно найти минимальное значение Р, чтобы неравенство выполнялось. Если мы поделим обе части неравенства на 2, получим Р > (3А - 10)/6.
Таким образом, диапазон возможных значений переменной Р, при которых неравенство А - 3Р < 10 будет выполняться, можно записать как Р > (3А - 10)/6.
Надеюсь, что это подробное решение помогло вам понять, как получить данный результат. Если у вас возникнут дополнительные вопросы, пожалуйста, не стесняйтесь задавать их.