Необходимо решить пределы.
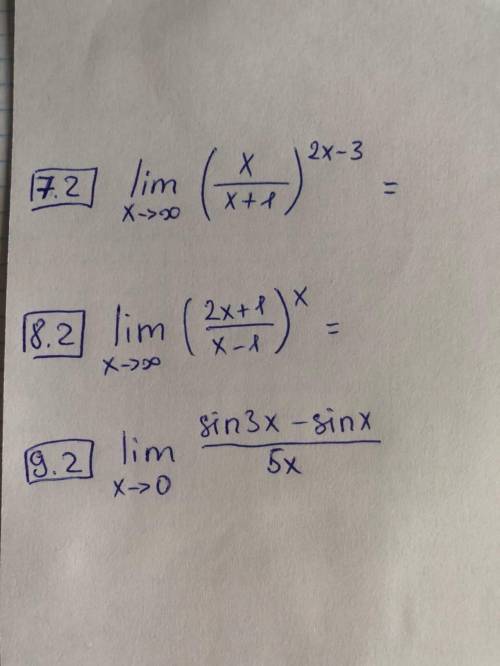
Другие вопросы по теме Математика
Популярные вопросы
- Как переводятся на слова талантливый и коротышка?...
3 - Владимир дубровский отказался отомстить троекурову, потому что:...
3 - Кто заботится о марии когда она покинула храм каким образом он был выбран...
2 - Природа россии № 1 1. высочайшая точка россии: а) белуха б) эльбрус в)победа...
2 - Во сколько раз мультфильм шел дольше прогноза погоды.если мультфильм смотрели...
1 - Запиши слова обозначающие комнаты в разных учреждениях в гостинице в поезде...
3 - 1.кінцівки риб? 2.гідростатічний апарат кісткових риб? 3. відкладення ікри...
3 - Заполните пропуски формами глагола to be. 1. her brother always very polite....
3 - Стены какого храма украшают фрески с изображением семьи ярослава мудрого?...
3 - Спишите,вставьте пропущенные запятые,укажите главные члены и вид каждого предложения...
1
ответ: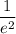
ответ: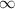
Примечание. В заданиях 7.2 и 8.2 воспользуйтесь вторым замечательным пределом:
А также следует воспользоваться эквивалентными бесконечно большими:
ответ: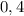
Примечание. В задании 9.2 воспользуйтесь первым замечательным пределом:
Граница суммы: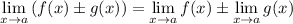
А также воспользуйтесь эквивалентными бесконечно малыми: