Не смог найти подобных решений задания

Другие вопросы по теме Математика
Популярные вопросы
- Замените глагол быть синонимом. образец: он был в городе. - он находился в...
3 - Расскажите как распределялась бы тепло на поверхности земли если бы наклона...
2 - Незадовго до смерті гетьман б. хмельницький заповідав своєму війську й товариству...
1 - Длины сторон прямоугольника - взаимно обратные числа. одна из них равна 6/17...
3 - Почему у детей больше прав, чем у взрослых?...
2 - Характиристика зоны пустынь по плану зарание...
2 - Мир без нефти. мини-! , уже второй раз спрашиваю....
1 - Вирушаючи в похід туристи позначили свій маршут на плані загальна довжина...
3 - Постройте в одной и той жк системе координат графики функциий y=-x+6...
3 - Что происходило в москве в 1156 году?...
3
докажем, что ρ является отношением эквивалентности.
1) рефлексивность: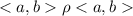
2) симметричность: если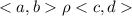
то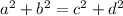
то есть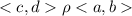
3) транзитивность: если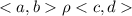 и
и 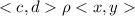 , то
, то
то есть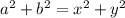
то есть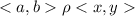
На координатной плоскости: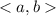 , если первый параметра a отождествить с вещественными числами оси Ox, а второй параметр b отождествить с вещественными числами оси Oy, тогда значениям a² + b² будет соответствовать окружность радиуса R≥0. То есть отношение эквивалентности ρ разбивает всю координатную плоскость на классы эквивалентности. Каждому классу эквивалентности соответствует окружность радиуса
, если первый параметра a отождествить с вещественными числами оси Ox, а второй параметр b отождествить с вещественными числами оси Oy, тогда значениям a² + b² будет соответствовать окружность радиуса R≥0. То есть отношение эквивалентности ρ разбивает всю координатную плоскость на классы эквивалентности. Каждому классу эквивалентности соответствует окружность радиуса