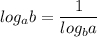не понимаю как решается
ОТВЕТ И ОБЪЯСНЕНИЕ
Другие вопросы по теме Математика
Популярные вопросы
- Какое из чисел 3.6 в 0 степени; 2.5 в 0,8 степени; 1.9 в -2 степени; 1.1 в...
1 - Решить групперовки 2ax+3by+6ay+bx...
2 - Какой согласный звук не имеет пары по звонкости-глухости?...
1 - 980081+(341640-1236*209)=? писменно...
1 - Приготовьте 100 г 2% раствора поваренной соли. как все расписать?...
2 - Переведите ! 1. мой друг- финансовый директор крупной корпорации. 2. через...
3 - Обяснить почему изменилась чистота пульса стоя и после 10 приседаний? надо...
1 - Водин день 4 дневных сеанса и3 вечерних на каждый дневной продали по 100билетов,а...
2 - Каково назначение плевральной полости?...
3 - Запиши одним словом,выдели корни. писатель,который пишет ; человек,который...
2
Прологарифмируем обе части равенства по основанию 11 .
Пользуемся свойством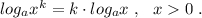
Перейдём от основания х к основанию 11 по формуле