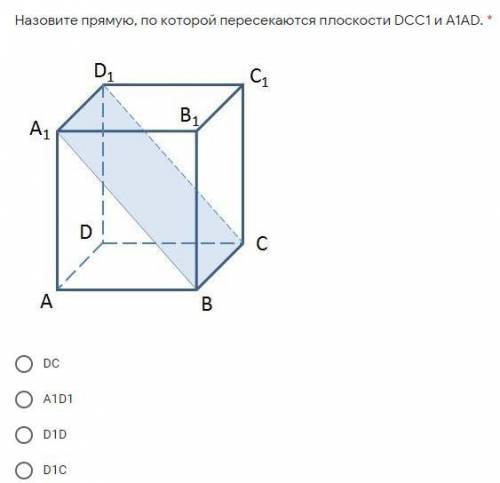
Назовите прямую, по которой пересекаются плоскости DCC1 и A1AD.

222222222и 33333333игггтгтнтнтннинмеам

Для понимания задачи, важно знать основные понятия. Плоскость - это геометрическая фигура, которая не имеет толщины и представляет собой бесконечное расширение в двух измерениях. Прямая - это наименьшая часть плоскости, ограниченная двумя точками.

В представленной задаче есть две плоскости: DCC1 и A1AD. Нам нужно найти прямую, по которой эти плоскости пересекаются.

Посмотрим на картинку. На ней изображены две плоскости - DCC1 (зеленая плоскость) и A1AD (синяя плоскость). Причем обе плоскости заданы точками, которые на них лежат. Нам нужно найти прямую, которая проходит через точки пересечения этих двух плоскостей.

Для начала определим, что точек пересечения двух плоскостей может быть несколько или даже их может не быть вовсе. В данном случае, по визуальному анализу, кажется, что прямая пересечения существует.

Чтобы найти эту прямую, можно воспользоваться системой уравнений. Пусть (x, y, z) - координаты точки на прямой пересечения. Тогда мы можем записать систему уравнений, состоящую из уравнений действующих плоскостей:

Уравнение плоскости DCC1:
3x - 4y + z = -2

Уравнение плоскости A1AD:
2x - y + 3z = 1

Систему этих двух уравнений можно решить методом подстановки или методом сложения/вычитания.

Для удобства решения приведем уравнения к более простой форме, например, к каноническому виду.

Уравнение плоскости DCC1:
z = 2 - 3x + 4y

Уравнение плоскости A1AD:
z = (1 - 2x + y) / 3

Теперь подставим одно уравнение в другое:

2 - 3x + 4y = (1 - 2x + y) / 3

Умножим обе части уравнения на 3, чтобы избавиться от дроби:

6 - 9x + 12y = 1 - 2x + y

Сгруппируем переменные x и y:
-9x + 2x - 12y - y = 1 - 6

-7x - 13y = -5

Из этого можно выразить x через y:
x = (13y - 5) / 7

Теперь воспользуемся этим значением x и подставим его в уравнение плоскости DCC1:

z = 2 - 3(13y - 5) / 7 + 4y

Дальше можно упростить это уравнение и получить выражение для z через y.

Таким образом, мы получили параметрическое уравнение прямой, по которой пересекаются плоскости DCC1 и A1AD:

x = (13y - 5) / 7
z = 2 - 3(13y - 5) / 7 + 4y

Если нужно найти точки на прямой пересечения, можно подставить различные значения y и вычислить соответствующие значения x и z. Например, при y = 0, x = -5/7 и z = 12/7. Это одна из точек на прямой пересечения.

Надеюсь, этот объяснение помогло вам понять, как найти прямую пересечения двух плоскостей.