1. Математика
  2. Найти y и y (Найти производную

Найти y' и y'' (Найти производную параметрической функции 1-го и 2-го порядка). Калькулятор не использовать! Постараться максимально у полученный результат.

алексей750 алексей750    1   07.03.2020 00:10    0

Ответы
Полькаа1642 Полькаа1642  11.10.2020 20:35

y'=\dfrac{y'_t}{x'_t}=\dfrac{\dfrac{2t(1+t^2)-t^2\cdot 2t}{(1+t^2)^2}}{\dfrac{2(1+t^3)-2t\cdot 3t^2}{(1+t^3)^2}}=\dfrac{(2t+2t^3-2t^3)(1+t^3)^2}{(2+2t^3-6t^3)(1+t^2)^2}=\dfrac{t(1+t^3)^2}{(1-2t^3)(1+t^2)^2}

y''=\dfrac{(y'_t)'_t}{x'_t}=\dfrac{\left(\dfrac{y'_t}{x'_t}\right)'_t}{x'_t}=\dfrac{\dfrac{y''_tx'_t-y'_tx''_t}{x'_t^2}}{x'_t}=\dfrac{y''_tx'_t-y'_tx''_t}{x'_t^3}    (2)

y''_t=\dfrac{2(1+t^2)^2-2t\cdot 2(1+t^2)\cdot 2t}{(1+t^2)^4}=\dfrac{2+2t^2-8t^2}{(1+t^2)^3}=\dfrac{2-6t^2}{(1+t^2)^3}

x''_t=\dfrac{-8t(1+t^3)^2-(2-4t^3)\cdot 2(1+t^3)\cdot3t^2}{(1+t^3)^4}=\dfrac{-8t-8t^4-12t^2+24t^5}{(1+t^3)^3}

Нашли все производные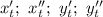 x'_t;~ x''_t;~ y'_t;~ y''_t, осталось подставить в формулу (2) и всё.

Максимально упрощенное выражение:

y''=\dfrac{(6t^8-4t^7+14t^6-13t^5-4t^4-5t^3-t^2-1)(t^3+1)^3}{2(t^2+1)^3(2t^3-1)^3}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
хели3 хели3  12.07.2019 11:40
Составь выражение и вычисли их значения.к частному чисел 45 и 5 прибавить произведение чисел 7 и 4...
darikesa69 darikesa69  12.07.2019 11:40
Поезд длиной 150м проходит мост за 28 сек, а мимо столба -за 10 сек найдите длину моста. (поставлю на акк если решишь)...
ldudin ldudin  12.07.2019 11:40
Решите : на рынок 48кг слив в ящиках, по 8кг в каждом, и столько же ящиков груш, по 9кг. сколько кг груш ?...
mayorova4 mayorova4  12.07.2019 11:40
Запишите в виде не правильной дроби смешанные числа 4 5/7, 6 5/12,3 4/8. натуральные числа 4 и 15 со знаменателем 9 описать каждое действие...
Vasya1godik Vasya1godik  12.07.2019 11:40
Сколько кубических сантиметров в трёх кубических дециметрах...
YuraJuliya YuraJuliya  12.07.2019 11:40
Смесь, состоящая из 3 частей цейлонского чая и 4 частей индийского, имеют массу 210 грамм. сколько граммов цейлонского чая в этой смеси? условие и решение...
tima3002 tima3002  12.07.2019 11:40
(1820х9х8-76+9383-315-548х7): 4=? 15290: 5+(10890-51+36616-27х10-154)х7=? , над щас...
ALESHABELAVIN ALESHABELAVIN  12.07.2019 11:40
Для изготовление папок приготовили 50 листов бумаги.они сделали 8 папок расходуя на каждую по 4 листа бумаги.ск листов бумаги у осталось....
ruslan189kalin ruslan189kalin  12.07.2019 11:40
Объём ящика, имеющего форму прямоугольного параллелепипеда, равен 60 см6. площадь крышки 20 см2. площадь меньшей боковой стенки 12 см2. найти площадь полной поверхности...
Veronika691 Veronika691  12.07.2019 11:40
За несколько часов турист должен пройти 35 км.через пять часов после начала движения ему осталось пройти еще 10км.за сколько часов турист пройдет оставшийся путь,если...

Популярные вопросы