Найти все значения параметра а, при которых уравнение имеет решение.

Другие вопросы по теме Математика
Популярные вопросы
- С ЗАДАЧЕЙ ЗАДАЧА В ПАСКАЛЬДано натуральное число n. Вычислить сумму первых...
2 - Повесть Алые парусаА.Грин...
3 - Выпишите цитату В. Яна, приведённую в конце вступительной статьи.выделите...
3 - 1. Опираясь не прочитанный текст, составьте и запишите распорядок обычного...
3 - умоляюread the text complete the gags (1-10) with the correct missing word...
2 - Поставьте сказуемое в Past Simple My family (see) a new film yesterday Our...
3 - Прочитайте фразы и тигрёнку написать эти глаголы в настоящем времени времени,используя...
2 - Какие предлоги употребляются в страдательном залоге и какое значение они...
3 - (а+1)(а-1)(а^+а+1)(а^-а+1) у выражения...
1 - 2** Order the words to make a short email.going/ Hi/it / Stefan /? / how...
2
Попробуем решить задачу в лоб.
ОДЗ: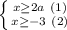
Возведём обе части в квадрат:
Возведём это всё ещё раз в квадрат:
Линейное уравнение всегда имеет ровно один корень. Осталось проверить, существует ли этот корень:
Условие 1:
Условие 2:
Условие 3:
ответ:![[-\frac{19}{2};\frac{13}{2}]](/tpl/images/0460/7008/e44bd.png)