Найти все значения a, при каждом из которых уравнение 2|x| - (x+a) = 0 имеет единственное решение на интервале (-1;1)

При , очевидно, уравнение имеет ровно одно решение -  , попадающее в заданный интервал. Соответственно, данное значение параметра пойдет в ответ.

Далее рассмотрим два случая:

Предположим, корни уравнения - отрицательные, т.е. . Уравнение принимает вид:

.

Проверяем найденный корень на попадение в интервал :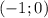

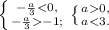
Предположим, корни уравнения - положительные, т.е. . Уравнение принимает вид .

Проверяем найденный корень на попадение в интервал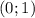 - очевидно, .

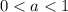Анализируем. Заметим, что значения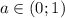 подпадают под оба случая: при таких значениях параметра на интервале существует как первый корень 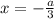, так и второй - . Т.к. корень должен быть всего один, все 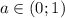   необходимо исключить из ответа.

Для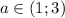 на отрезке существует только один корень - 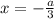, поэтому данные значения параметра идут в ответ.

ОТВЕТ: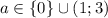 .