Найти все пары чисел (x, y), которые удовлетворяют уравнению 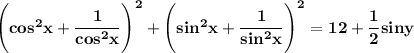
Другие вопросы по теме Математика
Популярные вопросы
- Пофантазируйте и напишите небольшое сочинение на тему: «если...
3 - Миша старше маши на 2 года а через 3 года сумма их возрастов...
3 - Автор либретто ко всем операм р. вагнера...
3 - Найдите область определения функции: y=1/x+6 (дробь)...
1 - Начертите угол mnk равный 150 градусов проведите биссектрису...
3 - Вычислите произведение а) 0,02*10 б)3,2 *100 в)0,3*1000 г) 2,39*1000...
1 - Мини сочинение маруся последние дни жизни...
1 - Из москвы в санкт-петербург выехали одновременно две машины:...
1 - C6h6+hno3→ 1.)что после реакции 2.)назвать вещества 3.)расставить...
2 - Постройте равнобедренный непрямоугольный треугольник (любой)....
2
По неравенству Коши между средним арифметическим и средним геометрическим
причем неравенство превращается в равенство, когда
первая скобка в ноль не обращается, а вторая равна нулю, когда
ответ: