найти все натуральные значения n удовлетворяющие уравнению 2022[nsqr(1011^2+1)]=n[2022sqr(1011^2+1)] , где [х] - наибольшее целое числоне превосходящее числа.

Ответы

sofia200000 30.01.2022 22:00

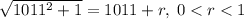Пусть $\sqrt{1011^2+1} = 1011+r,\; 0$ . Заметим, что 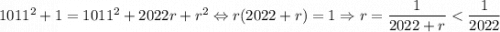$1011^2+1=1011^2+2022r+r^2 \Leftrightarrow r(2022+r)=1 \Rightarrow r = \dfrac{1}{2022+r} < \dfrac{1}{2022}$ , поэтому $\left[2022\cdot \sqrt{1011^2+1}\right] = \left[2022\cdot 1011+2022r\right] = 2022\cdot 1011$ . Тем самым уравнение перепишется в виде $2022\cdot \left[n\cdot\sqrt{1011^2+1}\right] = 2022\cdot 1011\cdot n \Leftrightarrow \left[n\cdot\sqrt{1011^2+1}\right] = 1011\cdot n$ .

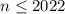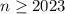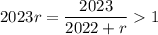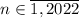Теперь подход примерно такой же: $\left[1011n+nr\right] = 1011 n$ . Если $n\leq 2022$ , то равенство выполняется. Пусть $n\geq 2023$ . Тогда $2023r = \dfrac{2023}{2022+r}1$ , значит, равенство выполняться уже не будет. Получаем, что решениями будут натуральные числа $n\in\overline{1,2022}$ .

ПОКАЗАТЬ ОТВЕТЫ

kamilachelny 30.01.2022 22:00

1;2;...;2022

Пошаговое объяснение:

Заметим:

$1011=\sqrt{1011^2}$

Отсюда

$2022\cdot 1011$

Но это означает, что

$\left\lfloor2022\cdot\sqrt{1011^2+1}\right \rfloor=2022\cdot 1011$

Значит, уравнение равносильно

$2022\cdot\left\lfloor n\cdot\sqrt{1011^2+1}\right \rfloor=n\cdot 2022\cdot 1011$

$\left\lfloor n\cdot\sqrt{1011^2+1}\right \rfloor=n\cdot 1011$

Если решения данного уравнения существуют, то, по определению дробной части числа, верно неравенство

$n\cdot\sqrt{1011^2+1}-n\cdot 1011\leq 1\\ n\leq \dfrac{1}{\sqrt{1011^2+1}-1011}=\dfrac{\sqrt{1011^2+1}+1011}{1011^2+1-1011^2}=\sqrt{1011^2+1}+1011$

$n\in N\Rightarrow n\leq 2022$

Но для таких значений переменной верны неравенства

$n\cdot 1011< n\cdot\sqrt{1011^2+1}То есть [tex]\forall n\in N, n\leq 2022$ по определению целой части числа равенство $\left\lfloor n\cdot\sqrt{1011^2+1}\right \rfloor=n\cdot 1011$ верно. Значит, все натуральные значения $n\leq 2022$ являются корнями данного уравнения.