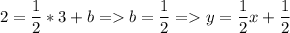Найти уравнение прямой проходящий через точку C( 3, 2) перпендикулярно к прямой y = -2x - 5
Другие вопросы по теме Математика
Популярные вопросы
- Чтобы измерить температуру человеческого тела, приходится держать термометр...
1 - Определите число молекул кислорода в 1 м3, если давление равно 77 кПа, а средняя...
2 - Какое давление на стенки сосуда производит водород, если число молекул в 1...
1 - При какой температуре молекулы кислорода имеют такую же среднюю квадратичную...
1 - На рисунке 3.24 показан график изменения состояния идеального газа в координатах...
2 - Изобразите на графиках в координатах р, V; р, Т и V, T изобарный процесс:...
1 - Два сосуда объемом V1 = 200 см3 и V2 = 100 см3, наполненные кислородом при...
3 - На стенку площадью S налетает поток молекул со средней скоростью . Число молекул,...
2 - Узкая вертикальная трубка длиной L, закрытая с одного конца, содержит воздух,...
1 - Изобразите на графиках в координатах р, V; р, Т и V, Т изотермический процесс...
3
Прямые y=k₁x+b₁ и y=k₂x+b₂ взаимно перпендикулярны, если
k₁·k₂=-1
y = -2x - 5⇒ k₁=-2 тогда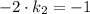
Точка C (3;2) принадлежит этой прямой
Подставляем координаты в уравнение и находим b₂
О т в е т.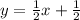
Прямые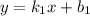 и
и 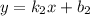 перпендикулярны, когда
перпендикулярны, когда 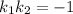
Пусть искомое уравнение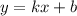
Тогда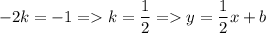
График проходит через C( 3, 2), значит