Найти уравнение прямой, проходящей через точку (2;1) параллельную прямой соединяющей точки (-2;3) и (-3;2)

Question

Математика: Найти уравнение прямой, проходящей через точку (2;1) параллельную прямой соединяющей точки (-2;3) и (-3;2)

Timm2517 · Answer

Даны две точки: (-2; 3) и (-3;2). График линейной функции имеет вид:

y = kx + b. Подставим точки. Получим:

3 = -2k + b и 2 = -3k + b. Получили систему:

$\left \{ {{-2k+b = 3} \atop {-3k+b=2}} \right.$

Вычтем из первого уравнения второе. Получим:

$\left \{ {{-2k+b +3k-b= 3-2} \atop {-3k+b=2}} \right. \left \{ {{k= 1} \atop {-3x+b=2}} \right. \left \{ {{k= 1} \atop {-3*1+b=2}} \right. \left \{ {{k= 1} \atop {b =5}} \right.$

Получили функцию:

y = x + 5

Дана одна точка: (2; 1). График линейной функции имеет вид:

y = kx + b. Подставим точки. Получим:

1 = 2k + b

Правило:

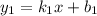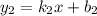Прямые y_1 = k_1x + b_1 и y_2 = k_2x + b_2 параллельны тогда, когда k_1 = k_2 .

y = x + 5, k = 1. Подставим:

1 = 2*1 + b

b = -1

Получили функцию: y = x - 1

Найти уравнение прямой, проходящей через точку (2;1) параллельную прямой соединяющей точки (-2;3) и (-3;2)

Популярные вопросы