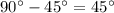Найти угол между осью оу ! и касательной к графику функции в y=f(x) в точке с абсциссой х=0 1)
Другие вопросы по теме Математика
Популярные вопросы
- радоаыладвща дог до вал сжалились д болд болд то двдвшвшвлаллалалаььц...
3 - Найти решение дифференциальных уравнений, удовлетворяющих заданным...
3 - УЗБЕКИСТАН АЛГЕБРА 7 КЛАСС НОМЕР 397 ВМЕ ПРИМЕРЫ РЕШИТЕ...
1 - Ищу друзей меня зовут:дашалет : 11ищу друзей от 11-14...
2 - Хелпаните на контроле сижу...
1 - Некоторое количество яиц нужно разложить в коробки по 10 штук в каждую...
2 - Нужна в решении.Огромная не пишите чепуху, все равно балы не засчитаю...
1 - ответьте на 1,4,5. вопрос....
1 - с решением 20б Всё на фото...
1 - Что можно узнать по отклонению листочков электроскопа: * а) увеличился...
3
Найдем теперь значение производной в точке х0=0
Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке. Следовательно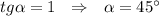 , значит угол между осью Оу равен
, значит угол между осью Оу равен