найти точки экстремума f(x)=2x^5-3x^4
Другие вопросы по теме Математика
Популярные вопросы
- Здравствуйте можете по географии? Задание 1. Определить. Оценка...
3 - Тите дробь.a® — 27B)а? + За +9°...
3 - Түзудің бойында: а) 3 нүкте; ә) 4 нүкте; б) 5 нүкте в) n нүкте...
2 - Составить тезисный план отражение в зерколе ...
2 - какую сумму оплатит клиент ФГУП почта России при осуществлении...
3 - (3-4i)x(-5+7i) комплексные числа...
3 - 2. Заполнить схемы -деление на отрасли «физической географии»...
3 - Укажите степень данного уравнения: x3y2 + 2xy – 7x4y = 0....
1 - Найди последнии цифру 3^246...
2 - Отметьте три точки A, B и C не лежащаю на одном прямой, и проведите...
2
Решим уравнение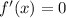 чтобы найти точки подозрительные на экстремум.
чтобы найти точки подозрительные на экстремум.
Как можно видеть из рисунка локальный максимум - x=0, локальный минимум x = 6/5