1. Математика
  2. Найти тангенсы внутренних

Найти тангенсы внутренних углов треугольника abc с вершинами в точках
а(1; 2) в(11; -3) с(7; 5)

стас488 стас488    3   27.10.2019 21:20    3

Ответы
Aysyiu Aysyiu  10.10.2020 09:56

tgA=\frac{4}{3}\\tgB=-\frac{3}{4}\\tgC - не определен (C=90°)

Пошаговое объяснение:

1) Получим уравнения трех прямых треугольника по формуле для прямой, проходящей через две точки:

\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}

Первая пара точек A,B:

l_{1}: \frac{x-1}{11-1}=\frac{y-2}{-3-2} ⇒ \frac{x-1}{10}=\frac{y-2}{-5}

Приведем уравнение к виду:

y=kx+b

\frac{x-1}{10}=\frac{y-2}{-5} ⇒ y=-\frac{1}{2}x+\frac{5}{2}

Вторая пара точек А,С:

l_{2}: \frac{x-1}{7-1}=\frac{y-2}{5-2} ⇒ \frac{x-1}{6}=\frac{y-2}{3}

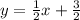
⇒ y=\frac{1}{2}x+\frac{3}{2}

Третья пара точек B,C:

l_{3}: \frac{x-11}{7-11}=\frac{y-(-3)}{5-(-3)} ⇒ \frac{x-11}{-4}=\frac{y+3}{8} ⇒ y=-2x+19

---

Теперь найдем тангенсы углов по формуле:

tga=\frac{k2-k1}{1+k1k2} , где k1 \ , \ k2 - коэффициенты в уравнении прямых.

tgA - угол между прямыми AB и AC (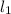l_{1} и l_{2}):

tgA=\frac{k2-k1}{1+k1k2}=\frac{\frac{1}{2}-(-\frac{1}{2})}{1+(-\frac{1}{2})\cdot \frac{1}{2}}=\frac{1}{\frac{3}{4}}=\frac{4}{3}

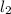tgB - угол между прямыми AB и BC (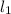l_{1} и l_{3}):

tgB=\frac{k2-k1}{1+k1k2}=\frac{-2-(-\frac{1}{2})}{1+(-\frac{1}{2})\cdot -2}=\frac{-1,5}{2}=-\frac{3}{4}

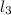tgC - угол между прямыми AC и BC (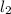l_{2} и l_{3}):

tgC=\frac{k2-k1}{1+k1k2}=\frac{-2-\frac{1}{2}}{1+\frac{1}{2}\cdot (-2)}=\frac{-2,5}{0}\\

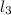Здесь 0 в знаменателе означает, что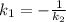 k_{1}=-\frac{1}{k_{2}}, а это условие перпендикулярности прямых. То есть угол C равен 90°.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
ivankirichko2 ivankirichko2  20.10.2020 15:56
Стороны параллелограмма относятся как 4:1, а его P=80 см. Найдите стороны параллелограмма. (plz можно только дано, но если хотите то и решение) ​...
ЛизаМэй ЛизаМэй  20.10.2020 15:56
Описать следующие информационные запросы на языке теории множеств: Найти множество персональных компьютеров, хранящихся на складе более 3 лет, за исключением ноутбуков, с объемом...
Nastya4816 Nastya4816  20.10.2020 15:56
А) Узнай объем коробки, если ее длина 12 см, ширина - 7 см, высота - 4 см.6) Найди сумму площадей боковых гранейи дна данной коробки.в) Узнай в различных источниках возможныеразмеры...
GlaydoN GlaydoN  20.10.2020 15:56
На рисунке изображены три маленьких квадрата внутри большого квадрата. Найдите длину отрезка, обозначенного знаком «?»...
YNWA12 YNWA12  20.10.2020 15:56
На бумажном квадрате 6×6 Дима закрашивает часть клеток. Потом Алёна берёт его квадрат и перегибает квадрат по центральной линии, затем разгибает его и перегибает второй раз...
fdgtrg4gewf fdgtrg4gewf  06.08.2019 10:00
Побудуй прямокутник abcd зi сторонами 2см i 4см знайти його периметр...
Словарь11 Словарь11  06.08.2019 10:00
Рост колиного папы 1 м 78 см. рост коли 120 см. на сколько сантиметров коля ниже папы?...
rusakova09 rusakova09  06.08.2019 10:00
Выполните действие и сократите результат: 1) 25 34-ых - 8 34-ых, 2) 12 целых 43 56-ых - 7 целых 22 56-ых. кто не понял пишите в комменты....
proha777 proha777  06.08.2019 10:00
Найди периметр и площадь квадрата, если длина одной стороны равна 3 см...
Бесполезная3 Бесполезная3  06.08.2019 10:00
Животные, навсегда исчезнувшие с лица земли...

Популярные вопросы