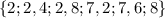Найти сумму всех решений неравенства
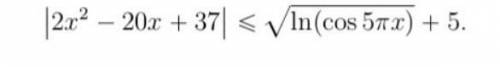
Другие вопросы по теме Математика
Популярные вопросы
- 5) Complete the sentences with your ideas.1 I like ...5 I need ...2 I love...
3 - 5x²+x-6=04x²+3x-7=02x²-5x+3=0 ...
2 - Виразивши в рівнянні змінну x через змінну y ,знайдіть 3 будь яких розв...
3 - Решите сложения системное уровеение: {3x-4y=20 {x+2y=0...
3 - Сделайте фонетический разбор слова всего ...
3 - Решите уравнение 3/4-(x+1/12)=1/5...
2 - Как изменяется радиус атома в группах с увеличением порядкового номера?...
1 - Напишите уравнение гидролиза соли. Определите реакцию среды водного раствора...
2 - Вопрос: вот как к тебе подойти и начать разговор? Как ответить?...
3 - Белгысыз бурышты табындар А=45 в-? С-? ...
3
ОДЗ:
так как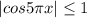 , то
, то
Тогда неравенство принимает вид:
C учетом ОДЗ: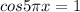
находим те корни этого тригонометрического уравнения, которые
удовлетворяют найденному решению![x \in [2;3]\cup[7;8]](/tpl/images/1361/0587/18aed.png)
При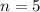
При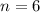
При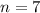
При
При
При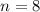
О т в е т.