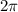Найти сумму всех корней уравнения cos^{4}x-sin^{4}x=1, принадлежащих промежутку [0;2п] Под п я иммею ввилу число пи, я не знаю как на клаве его вписать)
Другие вопросы по теме Математика
Популярные вопросы
- Найдите неизвестное число. x×100=3200,a×50=1000,x×5=300,m×80=800....
1 - Найдите синус,косинус и тангенс угла aom,если o-начало координат,а точки...
2 - Сделать трудовое обучение обслуживающий труд практическую работу 16...
1 - Из держ.підсумкової атестації вибери 1 рядок, усі слова якого є спільнокореневі....
2 - Верно ли, что: 10! = 10 х 9! 10! = 2! х 5! 12! 11! = 12?...
2 - Лучше писать ,писать и писать хоть он не пишет или оставить ?...
3 - Кому не сложно 15 предложений из с дефисным , слитным и раздельным написанием...
2 - Какой цифрой оканчивается разность квадратов двух трехзначных чисел одно...
3 - Закодируй в виде ребуса слова: вазон, семья, ус, сова, вода...
1 - Составьте кроссворд по теме дни недели , цвета на и составьте 5 предложений...
2
Используем формулу разности квадратов, основное тригонометрическое тождество и формулу двойного угла косинуса и все
ответ: