1. Математика
  2. Найти сумму степенного

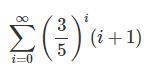
Найти сумму степенного ряда


Найти сумму степенного ряда

roma34569 roma34569    2   29.06.2020 21:54    1

Ответы
kuznecovamargo kuznecovamargo  30.08.2020 12:55

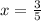
Пусть x=\frac{3}{5}

\sum\limits_{i=0}^{\infty} (i+1)x^i = \sum\limits_{i=0}^{\infty} (x^{i+1})'=(\sum\limits_{i=0}^{\infty} x^{i+1})' = (\frac{x}{1-x})' = (-1+\frac{1}{1-x})'=\frac{1}{(1-x)^2}

\sum\limits_{i=0}^{\infty} (\frac{3}{5})^i(i+1) = \frac{1}{(1-\frac{3}{5})^2}= \frac{25}{4}

ПОКАЗАТЬ ОТВЕТЫ
daurova2007 daurova2007  30.08.2020 12:55

25/4

Пошаговое объяснение:

Рассмотрим степенной ряд вида: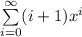 \sum\limits_{i=0}^{\infty} (i+1)x^i

По признаку Даламбера и необходимому условию сходимости ряда можно заключить, что этот ряд сходится при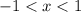 -1

Воспользуемся трюком с почленным интегрированием и дальнейшим почленным дифференцированием ряда, которые справедливы на промежутке сходимости исходного степенного ряда:

\sum\limits_{i=0}^{\infty} (i+1)x^i = \sum\limits_{i=0}^{\infty} (x^{i+1})'=(\sum\limits_{i=0}^{\infty} x^{i+1})' = (\frac{x}{1-x})' = (-1+\frac{1}{1-x})'=\frac{1}{(1-x)^2}

Подставляя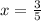 x=\frac{3}{5} находим сумму искомого ряда:

\sum\limits_{i=0}^{\infty} (\frac{3}{5})^i(i+1) = \frac{1}{(1-\frac{3}{5})^2}= \frac{25}{4}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
dsidorenko235 dsidorenko235  11.07.2019 09:50
Вb больших парт,а маленьких в n раз меньше.сколько всего парт в школу....
alusik2005 alusik2005  11.07.2019 09:50
Даужыня сшытка 20 см,а шырыня на 4 см меншая. чаму роуна сума даужынь усих старон сшытка...
vinnikdanil vinnikdanil  11.07.2019 09:50
Неполное частное q, если a=597, b = 12, r=9...
Iranmlp Iranmlp  11.07.2019 09:50
Стурбазы в одном направлении одновременно вышли два туриста со скоростями 3,5 километров час и 4,2 километров час какое расстояние будет между туристами через 2 часа...
vikakotova3 vikakotova3  11.07.2019 09:50
Победитель соревнований в беге на дистанцию 1500 м бежал со скоростью 6 м / с . спортсмен ,который прибежал последним, бежал со скоростью 5 м/c .за сколько времени пробежал дистанцию...
Vitomalc777 Vitomalc777  11.07.2019 09:50
До завтра надо. на какой угол повернётся минутная стрелка за: 30 мин; 15мин; 10мин; 1мин?...
софи157 софи157  11.07.2019 09:50
Выполни деление и сравни решение примеров каждого столбика 672÷2,354÷3,476÷4...
WrestlerTeam WrestlerTeam  11.07.2019 09:50
Два квадрата сложили вместе и получили прямоугольник с периметром 36 см. найди периметр квадрата....
luya21 luya21  11.07.2019 09:50
Начерти прямоугольник со сторонами 6 см и 3 см.сколько квадратных сантиметров в п рямоугольнике?...
ангелок76 ангелок76  11.07.2019 09:50
Водной группе 36 девочек , а в другой 24 мальчика.их надо разделить на равные команды ,каждая из которых состоит или только из мальчиков ,или только из девочек.какое наибольшее число...

Популярные вопросы