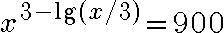
Математика: Найти сумму корней уравнения

Найти сумму корней уравнения

Ответы

Даниил12345666 15.10.2020 15:41

ОДЗ x>0

Немного преобразуем

$\displaystyle\\x^{3-\lg(x/3)} = x^{3+\lg 3 - \lg x}\equiv x^{A-\lg x} = 900$

Где введено обозначение A = 3+ lg3, 3<A<4.

x=1 очевидно не подходит как корень. Исключая из ОДЗ x=1, возьмем логарифм по основанию x от обеих частей

$A - \lg x = \log_x 900 = \lg 900 / \lg x$

Отметим что

$\lg 900 = 2 + \lg 9 = 2+2\lg 3 = 2A - 4$

Переобозначим lg x = u

$\displaystyleA - u = (2A-4)/u\\u^2-Au+2A-4 = 0\\u = \frac{A\pm\sqrt{A^2-8A+16}}{2}\\u_1 = A-2; u_2 = 2$

Вернемся к исходной переменной

$\lg x = A-2 = 1+\lg 3 = \lg 30; x=30\\\lg x = 2; x=100$

Сумма корней = 130

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

Ботакан17 10.09.2019 12:40

неудачник16 10.09.2019 12:40

Найдите значение выражения: 75: 15-828: 92. !...

yakirill0109200 10.09.2019 12:40

Rikrbrujrh 10.09.2019 12:40

artem24322004 10.09.2019 12:40

Найти производные функции y=3x^2-6x+7/x^2...

йцукенг27 10.09.2019 12:40

Найди периметр фигуры со сторонами 10см, 7см, 10см, 3см...

Madinauakhitova 10.09.2019 12:40

75минус 15: 5+10 скобки равняется22...

кпрооо 10.09.2019 12:40

Horvatskiy 10.09.2019 12:40

Решить уравнения 1)9^x=27^(x-2) 2)0,4^(x^2-1) 1 3)4^x+3*2^x-4=0...

alexvip7777ap 10.09.2019 12:40

Какие есть механические обработки круп? мне....