1. Математика
  2. Найти sin α и cos α, если tg α/2  =

Найти sin α и cos α, если tg α/2  = 5.

GenaTurboKrytt GenaTurboKrytt    2   14.03.2022 02:14    7

Ответы
durindub007 durindub007  19.03.2022 12:20

\sin{\alpha}=\dfrac{5}{13},\cos{\alpha}=-\dfrac{12}{13}

Пошаговое объяснение:

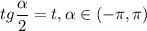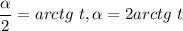Пусть tg\dfrac{\alpha}{2}=t,\alpha\in (-\pi,\pi). Тогда \dfrac{\alpha}{2}=arctg\ t, \alpha =2arctg\ t.

\sin{\alpha}=\sin{(2arctg\ t)}=2\cdot\sin{arctg\ t}\cdot\cos{arctg\ t}

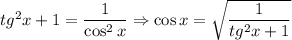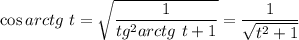
Найдём синус и косинус от арктангенса. Поскольку tg^2{x}+1=\dfrac{1}{\cos^2{x}}\Rightarrow \cos{x}=\sqrt{\dfrac{1}{tg^2{x}+1}}, то \cos{arctg\ t}=\sqrt{\dfrac{1}{tg^2arctg\ t+1}}=\dfrac{1}{\sqrt{t^2+1}}

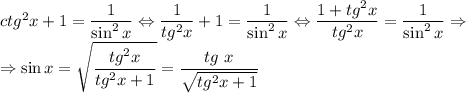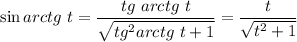Поскольку ctg^2{x}+1=\dfrac{1}{\sin^2{x}}\Leftrightarrow \dfrac{1}{tg^2{x}}+1=\dfrac{1}{\sin^2{x}}\Leftrightarrow \dfrac{1+tg^2{x}}{tg^2{x}}=\dfrac{1}{\sin^2{x}}\Rightarrow\\\Rightarrow \sin{x}=\sqrt{\dfrac{tg^2{x}}{tg^2{x}+1}}=\dfrac{tg\ x}{\sqrt{tg^2{x}+1}}, то \sin{arctg\ t}=\dfrac{tg\ arctg\ t}{\sqrt{tg^2{arctg\ t}+1}}=\dfrac{t}{\sqrt{t^2+1}}.

Получаем: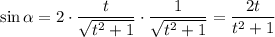 \sin{\alpha}=2\cdot\dfrac{t}{\sqrt{t^2+1}}\cdot\dfrac{1}{\sqrt{t^2+1}}=\dfrac{2t}{t^2+1}

\cos{\alpha}=\cos{(2arctg\ t)}=\cos^2{arctg\ t}-\sin^2{arctg\ t}=\left(\dfrac{1}{\sqrt{t^2+1}}\right)^2-\\ -\left(\dfrac{t}{\sqrt{t^2+1}}\right)^2=\dfrac{1}{t^2+1}-\dfrac{t^2}{t^2+1}=\dfrac{1-t^2}{1+t^2}

При t = 5: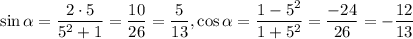 \sin{\alpha}=\dfrac{2\cdot 5}{5^2+1}=\dfrac{10}{26}=\dfrac{5}{13},\cos{\alpha}=\dfrac{1-5^2}{1+5^2}=\dfrac{-24}{26}=-\dfrac{12}{13}

P. S. Эта замена (через тангенс половинного угла) называется универсальной тригонометрической подстановкой.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
stasgura stasgura  12.09.2019 07:10
Кто сдает огэ? подскажите, , сколько нужно на огэ по , чтобы сдать на 5. я почему-то всегда думал, что 22 достаточно, а сегодня учительница сказала: не 22, а 25...
гарристайлсс гарристайлсс  12.09.2019 07:10
Выполните деление с остатком 139.169 на 45 455 168.627 на 54...
pbavaМАНЯ pbavaМАНЯ  12.09.2019 07:10
Точкa m сpeдняя точкa стоpоны ab. нaйдитe paсстояниe мeжду точкaми cm...
Zlyka11 Zlyka11  12.09.2019 07:10
Із 9 грам дроту можна зробити 5 гачків.скільки гачків можна зробити з 27 г дроту?...
dsklim2oxkfup dsklim2oxkfup  12.09.2019 07:10
Выразите в метрах 15км 2км 500м 6км 90м выразите в километрах и метрах 1840м 7035м выразите в сантиметрах 3дм 8см 1м 68см 7м 5см 70мм 980мм выразите в сантиметрах...
Onewood Onewood  12.09.2019 07:10
С2 участков собрали 44 мешка лука по 20 кг в каждом сколько мешков лука собрали с первого участка если со второго было собрано на 360 кг лука меньше?...
mrmistik41 mrmistik41  12.09.2019 07:10
1.можно ли построить треугольник со сторонами 1) 3 см 4 см 1 см 2)6 см 7 см 8 см 3)15 см 20 см 25 см 4)12 см 5 см 6 см...
astashkin222 astashkin222  12.09.2019 07:10
Примеры с обьяснениями 50-46, 70-38, 50-6, 70-8 ,90-24 ,94-20, 100-2, 100-38...
kisik404 kisik404  12.09.2019 07:10
Чем опасны потёкшие батарейки с истёкшим сроком годности....
ударник52 ударник52  12.09.2019 07:10
Рещите лёгкое кровнение 4 класса 9а= 621...

Популярные вопросы