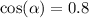
Найти sin a, tg a^2
Очень
Другие вопросы по теме Математика
Популярные вопросы
- Как одуванчик при к перезимовке ?...
3 - Катер км по течению реки и столько же обратно, затратив на весь путь 1 час 45 минут....
2 - Не изменяемые приставки. придумать слова на приставки: з,с пре, при написать всего...
1 - 1.острый угол прямоугольного треугольника равен 30 градусов а его гипотенуза равна...
2 - Из пункта а и в, расстояние между которыми 260 км, одновременно навстречу друг...
2 - Периметр равнобедренного треугольника равен 20см. его основание в два раза меньше...
2 - всех! 1. составьте предложение из рассыпавшихся слов: рождается,существо,как,личность,как,человек,и,биологическое,развивается....
1 - Нужно составить диалог на с кем либо на тему как я провел лето . в заранее !...
3 - Написать сообщение про открытия или изобретения 19века...
2 - Втреугольнике abc угол с равен 90 градусов, sina= 3/5, ac=3. найдите вс ответ должен...
2
Пошаговое объяснение:
В условии задачи не написано какой четверти принадлежит угол.
Будем считать, что угол острый и все тригонометрические функции его положительны.