Найти расстояние от точки (4; 0) до параболы 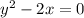 .
.
Другие вопросы по теме Математика
Популярные вопросы
- Для каких значений аргумента x являются положительными значениями функций y=2x+8...
3 - Эссе взаимосвязь функции и строение корня краткое...
2 - По результатам олимпиады 25% написали на оценку 5, 36% на 4, 12 учеников написали...
1 - Почему у слова короткий коротк это корень ? например: короткий путь....
2 - Чем отличалось положение человека отрабатывавшего долг от положения раба...
1 - День обломова по плану с ольгой или агафью...
1 - Сочинение по высказыванию дети - наш главный природный ресурc г. гувер. (по...
1 - Хто з врятованих був страшим за віком п ятнадцятирічний капітан...
2 - Из каких компонентов состоит внутренняя среда организма? как эти компоненты...
2 - Нам задали сочинение о болезни по следующим пунктам: 1. когда я заболел 2. какая...
2
Пошаговое объяснение:
на графике параболы найдем точку М1, наиболее приближенную к точке М(4;0) а потом посчитаем расстояние между этими точками
итак, на параболе берем точку М1(х; y) =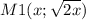
запишем расстояние между точками M1 и M
нам нужно, чтобы это расстояние было минимальным
мы имеем расстояние d²=x²-6x+16 и надо, чтобы оно → min
это будет там, где производная функции будет =0 (поскольку y₁ парабола ветвями вверх)
будет =0 (поскольку y₁ парабола ветвями вверх)
мы нашли точку М1(3;√6) на параболе у² = 2х наиболее приближенную к точке М(4;0)
теперь найдем расстояние между этими точками