Найти промежутки монотонности и точки экстремума функции y=3x^2-4x+5

Пошаговое объяснение:

Найдём производную: y'=6x-4, x ∈ R

Найдём нули производной: 6x-4=0; 6x=4; x=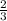

Нанесём точку на прямую и узнаем промежутки монотонности:

f(x) растёт на промежутке x ∈ (;+∞)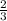

f(x) падает на промежутке x ∈ (-∞;)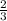

Точка х=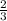 есть точкой экстемума минимума.