Найти производные 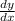 заданных функций.
заданных функций.
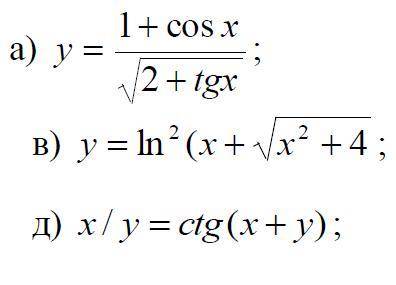
Другие вопросы по теме Математика
Популярные вопросы
- Утвори присвійні прикмeтники сeргій, донька, мeлашка, маланка,...
1 - Вычислить объем, число молекул и число атомов водорода (н) и...
1 - Ссинтактическим разбором этих предложений . лето чем ближе к...
3 - Вычислить объем, число молекул и число атомов водорода (н) и...
3 - 1.ситуация мяч в игре в волейболе 2.слово волейбол , ,...
3 - Составить характеристику володи и зинаиды из первая любовь тургенев....
1 - Письменный ответ на вопрос: что роднит стихотворение а.к.толстого...
1 - Для хранения растрового изображения размером 174×174 пикселей...
1 - Вычислить объем, число молекул и число атомов водорода (н) и...
3 - Сторони паралелограмма дорівнюють 15 см і 9 см. одна з діагоналей...
2
а)
последним действием почленно разделила
в)
д)