Найти производные y' =dy/dx заданных функций
Другие вопросы по теме Математика
Популярные вопросы
- Найдите значение выражения (4-у)²–у(у+1) при у= - 1 9...
1 - Перефразируйте эти предложения(из одного сделать два) в: а)условное наклонениеб)повелительное...
1 - (если что это с красной книги essential grammar in use, может у кого то...
3 - Яку роль у народжені західної культури відіграла церква ?...
1 - Найдите значение выражения tg(α+β)-cos(α+β)...
3 - Краткий пересказ параграфа по россии 8 класс, арсентьев, §22 внешняя политика...
1 - Скласти речення із словом how...
2 - Вычислите массу калия и 9%-ного раствора гидроксида калия, которые необходимы...
1 - Тема древняя греция. прочитайте список событий и напишите событие которое...
1 - Выражения 1. (а^-2)^-4*(а^3)^-2/(а^-3)^-1: (а^-1)^3 2. (3а^-1/5в^2)^-2:...
3
Пошаговое объяснение:
б)![\[{\mathop{\rm tg}\nolimits} y = xy + \ln xy;\]](/tpl/images/4978/4393/5ed2c.png)
Подразумеваем, что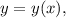 дифференцируем обе части по
дифференцируем обе части по 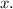
Так,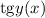 — сложная функция, поэтому ее производная это сперва производная от тангенса, умноженная на производную от его аргумента
— сложная функция, поэтому ее производная это сперва производная от тангенса, умноженная на производную от его аргумента 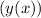 :
: 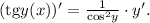
Находим производную xy как производную произведения: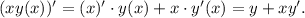
Производная логарифма — опять сложная функция: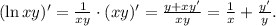
Вместе получаем: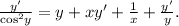
Выражаем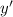 из последнего равенства. Можно преобразовать ответ, избавившись от «двухэтажных» дробей:
из последнего равенства. Можно преобразовать ответ, избавившись от «двухэтажных» дробей: 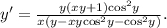
в)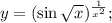
Прологарифмируем по натуральному основанию обе части данного равенства: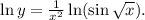 Теперь найдем производную от обеих частей аналогично решению п. б).
Теперь найдем производную от обеих частей аналогично решению п. б).