Найти производные следующих функций.полный ответ
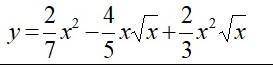
Другие вопросы по теме Математика
Популярные вопросы
- Диалог про человека который идет устраиваться на работу...
2 - Мне нужно составить на и с переводом 2 предложения present simpl 2на present...
1 - Закончить молекулярное и написать ионные уравнения рейкций hcl+ mgso4+ zn(oh)2+...
3 - Трем зайцам раздали 12 морковок поровну.сколько понадобится пяти зайцам? реши...
2 - Напишите сложные слова с соединительной гласной е, вторая основа вод е, вторая...
1 - Найти отгатку к четверостишью: она была растеньем в поле,и нитью плотного...
2 - Перенести слова со строчки на строчку фаэт, аталь,эолинь...
1 - Первый пятиугольник подели отрезком на треугольник и шестиугольник, второй-на...
3 - Склады речення зи словом снижок и ричка...
2 - Почему ядро, состоящее из одноименно заряженных протонов, не распадается?...
3
Пошаговое объяснение: