Найти производные первого порядка для заданных функций.(С решением
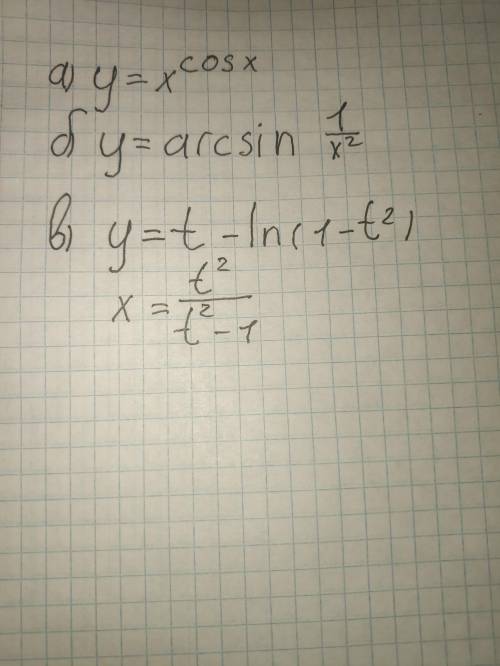
Другие вопросы по теме Математика
Популярные вопросы
- Дано abcd параллелограмм. угол b 120 градусов. угол 1 минус угол...
3 - Складіть рівняння реакцій добування фосфору з двох простих речовин...
3 - Я, смиренный, дедом своим ярославом, благословенным, славным, нареченный...
1 - Пересказ от имени алёши горького детство...
2 - Невідоме число збільшили у 7 разів і одержали 56.знайди невідоме...
1 - Решить тест ! p.s.: 30 (или сколько там даёт сайт)...
2 - Вправильной четырехугольной призме abcd a1 b1 c1 d1 ребро aa1 равно...
1 - Продолжите диалоги согласно ситуации. 20 оn a visit: josh: -hello!...
2 - Цепочка превращений нитробензол-реакция зинина-2 4 6 фениламин...
2 - Объяснить постановку знаков, язык,великолепный наш язык,речное...
2
а)
по формуле:
б)
в)
по формуле: