Найти производные: 1) y=x² · ∛x
2) y=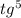 ·x
·x
3) y=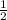 x²-
x²- 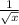 +
+ 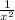 - 3
- 3
4) y= 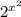 · arctg
· arctg 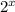
5) y= 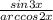
6) y=㏑ tg 2x
Другие вопросы по теме Математика
Популярные вопросы
- Оқулықтан тыс тапсырма/ задания внеучебника/ Жазбаша письменно 2-тапсырма...
1 - Вычеслите 481 задание 5 класс...
2 - 1. Титульний слайд. Заголовок слайда Збережемо природу України, підзаголовок...
3 - Изготовить 2 модели строения атома одного из 20 первых элементов...
3 - а) -2⁴/3 - 2⁴/9; б) (-2)²/2³- 5²/4...
1 - За яких умов хлор може окислити плюмбум до вищого ступеню окислення,...
2 - 502. школьники провели благотворительную акцию для дома престарелых...
1 - Определи, для разделения какой смеси применяется такой как выпаривание....
3 - 10-тапсырма. Мәтін бөліктерінің әрқайсысында қандай ақпарат айтылғанын...
1 - класс английский Биболетова ...
2
Пошаговое объяснение:
1.
2.
3.
4.
5.
6.