Найти производную от сложной функции:
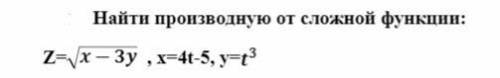
Другие вопросы по теме Математика
Популярные вопросы
- Найдите cos А, если: a) sin А = 1/3 ; б) sin А = √2/3....
2 - Найдите углы ромба, если его диагонали равны 2√3 и 2....
2 - В треугольнике ABC угол А равен 60°, АВ = 3 см, ВС = 4 см. Найдите АС....
2 - Существует ли угол А, для которого sin А = cos А?...
2 - В равностороннем треугольнике со стороной а найдите радиусы г и R вписанной...
1 - Найдите sin А, если: a) cos А = ½ б) cos А = √2/2....
3 - Докажите, что для любого острого угла А выполняются неравенства: a) sin А...
1 - Постройте угол, косинус которого равен: а) 3/5; б)4/9 в) 0,5; г) 0,8....
2 - Подобны ли: а) любые два эллипса; б) любые две...
2 - Найдите косинус угла в 18°....
3
Пошаговое объяснение:
формула для производной сложной функции нескольких переменных
функция задана в виде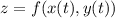 , тогда производная имеет вид
, тогда производная имеет вид
для нашего случая посчитаем
и тогда ответ
(здесь мы не будем заменять х на 4t-5, и у на t³, хотя и можно было. но, как правило, когда функция изначально предложена в "замысловатом" виде, то будет логичным оставить в таком же виде и результаты)