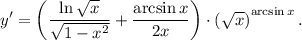Найти производную функции:
y=(sqrt(x))^arcsin(x)
Другие вопросы по теме Математика
Популярные вопросы
- - Решите уравнение 5 - 2х = 11-7(x+2)....
2 - 1. Разложите на множители: 1) 36m2 — 9n2 22 81m2 - (1 + Зm)2...
3 - Чим відрізняються підземні води від поверхневих...
2 - 2. Выпишите грамматическую основу из предложений (подлежащее и...
1 - 2. Построить график функции у=2х2 – 3х – 2. По графику определите...
1 - А-9, «Арифметическая прогрессия», В-21. 1. Найдите 3-й член арифметической...
1 - Проект цифровые копии больных Цель и задачатекста побольше...
3 - найти количество отрицательных элементов целочисленного массива....
3 - , юридическая ответственность, задание из огэ , всё на фото...
3 - 189. Выполните действия: а) 5 5/9+2 8/9; б) 7 1/12-4 5/12; в) 8...
1
Задание. Найти производную функции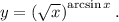
Решение. Задана функция вида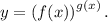
Для нахождения производной данной функции выполняют следующие этапы:
1. Прологарифмировать обе части данного равенства по основанию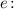
2. По свойству логарифмов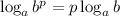 имеем:
имеем:
3. Найти производную двух частей равенства по переменной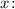
3.1. Используя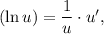 имеем:
имеем:
3.2. Используя правило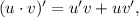 имеем:
имеем:
3.2.1. Используя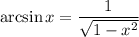 и
и 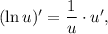 имеем:
имеем:
3.2.2. Используя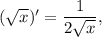 имеем:
имеем:
3.2.3. Упросим выражение и получаем:
3.3. Имеем:
4. Умножим обе части равенства на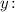
5. Поскольку из условия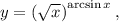 то:
то:
ответ: