1. Математика
  2. Найти производную функции:

Найти производную функции: y=ln(x/√(1+x^2))

kristina17102004 kristina17102004    2   16.09.2019 06:20    0

Ответы
ivan200302 ivan200302  07.10.2020 19:09
Сначала сделаем преобразования с логарифмом, чтобы проще брать производную. Выражение распадается на два логарифма. Производная первого - табличная, второго - тоже табличная, но т.к. функция сложная, то домножаем на производную функции под логарифмом.

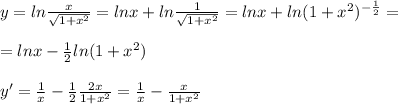
y=ln \frac{x}{\sqrt{1+x^2}} =lnx +ln \frac{1}{\sqrt{1+x^2}} = lnx +ln (1+x^2)^{- \frac{1}{2}} = \\ \\ = lnx - \frac{1}{2}ln (1+x^2) \\ \\ y' = \frac{1}{x} - \frac{1}{2}\frac{2x}{1+x^2} = \frac{1}{x} - \frac{x}{1+x^2}
ПОКАЗАТЬ ОТВЕТЫ
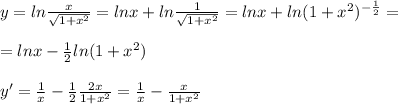
Другие вопросы по теме Математика
kaamazon kaamazon  01.12.2020 10:02
Машина каждый час двигалась либо только вперед, либо только назад, при этом, в сумме за 2 часа подряд она отъезжала назад на 10 километров. За 9 часов езды машина оказалась...
mariazhu mariazhu  01.12.2020 10:02
B парке осенью приготовили две клумбы прямоугольной и квадратной формы. У клумбы прямоугольной формы длина составляет 6 м, а ширина - 4 м. У клумбы квадратной формы сторона5...
SpaniGar SpaniGar  01.12.2020 10:02
у мальчика было несколько монет он потратил на булку 5 монет а на шоколадку 3 монеты и у него осталось 20 монет сколько всего было монет у мальчика...
дико64 дико64  01.12.2020 10:02
Периметр параллелограмма равен 46 см. Найдите стороны параллелограмма, если одна сторона на 5 см меньше другой. В ответ запишите длину большей стороны. ответ дайте в сантиметрах...
dyganovanton dyganovanton  01.12.2020 10:01
Медиана-это отрезок, который Делит треугольник пополам Делит сторону пополам Делит угол пополам Образует угол 90 градусов...
nlapenko nlapenko  01.12.2020 10:01
456. Используя формулу пройденного расстояния, найдите скорость и, если а) S = 450 км, t = 90 часов; б) S = 280 м, t=7 с.в) S = 180 км, t = 9 часов; г) S = 140 м, t = 28...
lermolen lermolen  01.12.2020 10:01
Тест Решение тригонометрических уравнений ​...
ВикторикаРоэн ВикторикаРоэн  01.12.2020 10:01
высота прямоугольного параллелепипеда равна 4 4/5 его длина в 3 3/8 раза больше высоты, а ширина составляет 20% длины. Вычислете обьём параллепипеда...
viktoriasvoya viktoriasvoya  01.12.2020 10:01
По значению одной из тригонометрических функций (sin α, cos α,...
Тогжан11111111 Тогжан11111111  01.12.2020 10:01
По значению одной из тригонометрических функций (sin α, cos α, , с) найти значения остальных трёх: п- число пи 1) cos a= -3/5 и п/2 2)sin a = -2/5 и п 3)tg a = 15/8 и п 4)ctg...

Популярные вопросы