Найти производную функции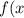=ln(8x^{2}+6x+2))
Другие вопросы по теме Математика
Популярные вопросы
- Вправильній чотирикутній піраміді ребра дорівнюють 5см,а периметр...
3 - 5ублей стоит 1 тетрадка , 6 рублей стоит 1 ручка сколько стоит...
3 - Найти площадь треугольника,вершины которого имеют координаты (-1;...
3 - Очем и чему учит рассказ островского снегурочка написать кратко...
3 - Анар за 4 дня прочитал 81 страницу. каково среднее количество прочитанных...
3 - 8в 14 степени ( 8 в 4 степени) в 5 степени (8 в 5 степени ) в 7...
3 - Очем и чему учит рассказ л.андреева ангелочек написать кратко...
3 - Краткое содержание платонов волшебное кольцо 5,6 предложений,кратко...
1 - Какую часть развернутого угла составляет 2 градуса , 16 градусов...
1 - Точки d и r являются основаниями высот остроугольного треугольника...
2
Производная сложных функций.
Пошаговое объяснение: