найти производную функции 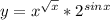 логарифмического дифференцирования
логарифмического дифференцирования
Другие вопросы по теме Математика
Популярные вопросы
- Как спешить слова в мен. сен. сыз ол. быз. сендер. сыздер....
1 - Периметр прямоугольника равен 528 см. длина 261 см найдите площадь прямоугольника...
1 - От худого семени. какого рода и числа?...
3 - Удівчинки стільки ж братів, стільки й сестер, а в хлопчика з цієї сімї братів...
1 - Угол а треугольник аbc на 55 градусов больше угра b и на 40 градуса меньше...
1 - Морфологический разбор слова далеко,вниз,вдоль....
3 - Сисследовать функцию на монотонность и построить график 6+12x -x^2...
3 - Решите про двух лыжников.там два вопроса значит должно быть два ответа. два...
3 - Антоним к словосочетанию свежий хлеб...
3 - Какое проверочное слово к слову башенные ( часы)...
2
Пошаговое объяснение:
получаем: