Найти производную функции: 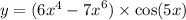
Другие вопросы по теме Математика
Популярные вопросы
- Опыт 1. Растворимость спиртов в воде В две пробирки налили по 2 мл...
3 - Магній→ хлорид → магній гідроксид→ магній оксид→ магній сульфат→ магній...
2 - Консументы 1 степени и 2 в ПУСТЫНЕ...
3 - Ребят по действиям и столбиком ❤ 13 a) 410. (95 + 28860 : 39) : 167...
3 - Накресліть коло та опишіть наволо нього шестикутник...
2 - Консументы 1 степени и второй в Долине Реки ИЛИ...
1 - Апавяданне пра сяброуства Стася и Мици апавяданне Страта...
2 - Упростите выражение 9+5sin^2α-5cos^2α...
1 - По одной из прочитанных книг, подготовить рассказ о жизни и отношениях...
3 - «Легион» – число, равное миллиону миллионов. Если разделить миллион...
3
возьмём производную от обоих частей
y`=D/dx ((6x⁴-7x⁶)*cos(5x))
используем правило дифференцирования
y`=d/dx(6x⁴-7x⁶)*cos(5x)+(6x⁴-7x⁶)*d/dx (cos(5x))
вычислим производную суммы или разности
y`=(6*4x³-7*6x⁵)*cos(5x)+(6x⁴-7x⁶)*(-sin(5x)*5)
упростим выражение
y'=(24x³-42x⁵)*cos(5x)+(6x⁴-7x⁶)*(-5sin(5x))
y'=(24x³-42x⁵)*cos(5x)+(6x⁴-7x⁶)*(-5sin(5x))