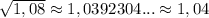Найти приближенное значение с производной:
sqrt(1,08)
Другие вопросы по теме Математика
Популярные вопросы
- Между сторогами развёрнутого угла aod проходят лучи ob и oc так что aob=53°...
2 - Спорт, наиельные украшения, компьютер, религиозные ритуалы, личное имя, фольклор,...
3 - Пришкольного участка ученики за 2 дня собрали 1260 кг картофеля во второй...
3 - За 30 монет купили 30 птахів. скільки купили птахів кожного виду, якщо за...
2 - Визначте,у якому масштабі відстань на мысцевості у 40 км відповідає відрізку...
3 - Предложите название статьи для научного журнала по теме: общественный строй...
3 - Расстояние 124km двух станций одновременно были два поезда в противоположных...
3 - Площадь прямоугольника 36 см, периметр 24 см. нужно найти стороны...
3 - Вкакую особую пару входят слова- свинья, полынья?...
1 - Назовите королей правящих во франции в 19 веке...
2
ответ: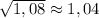 .
.
Пошаговое объяснение:
Проверим на калькуляторе: