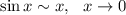Найти предел, не используя правило лопиталя
Другие вопросы по теме Математика
Популярные вопросы
- Как отличить наречия образ действия и мера?...
1 - ответить на вопросы: 1. годы жизни м. ю. лермонтова? 2. в каком селе детство...
1 - Выполни деление уголком 25623: 34 и пользуясь полученной записью найди значения...
1 - Впервый день на мельнице смололи 0,3 зерна,во второй день 0,3 остатка,в третий...
2 - Надо собрать пословицу из этих слов и,красный,пчела,цветок,на,летит...
1 - Уксусная эссенция продается расфасованная я в бутылке по 200 г . на этикетке...
2 - Gone,sue,today,has,shopping. нужно составить предложение из этих слов...
1 - Сочинение из 10 односоставных предложений на любую из этих тем: снег, зима...
1 - Скорость распространения волн 4 м/с ,частота равна 1,25 гц. определите длину...
2 - Как проверить слова: , ,сп..собности, )разному (не)ожида(н.нн)о,см.. ,выр..стал...
1
эквивалентность функции