1. Математика
  2. Найти предел функций двух переменных

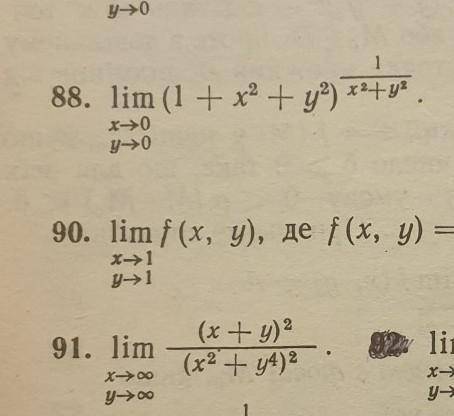
Найти предел функций двух переменных 88 и 91


Найти предел функций двух переменных 88 и 91

GLEBfy GLEBfy    1   24.08.2021 00:15    0

Ответы
bogdanmaltsev bogdanmaltsev  24.08.2021 01:00

88) e; 91) 0

Пошаговое объяснение:

88) Перейдем к полярным координатам:

\lim\limits_{x\to 0,y\to 0} (1+x^2+y^2)^{\frac{1}{x^2+y^2}}=\left[x=r\cos\varphi, y=r\sin\varphi\right]=\lim\limits_{r\to 0} (1+r^2)^{\frac{1}{r^2}}=e

91) Для достаточно больших значений y [на самом деле, можно явно указать, что |y|≥1, но такая конкретика здесь не важна] верно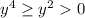 y^4\geq y^20.

Тогда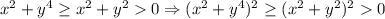 x^2+y^4\geq x^2+y^20\Rightarrow (x^2+y^4)^2\geq (x^2+y^2)^20, откуда, с учетом неравенства о средних,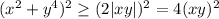 (x^2+y^4)^2\geq (2|xy|)^2=4(xy)^2

Но тогда

\dfrac{(x+y)^2}{(x^2+y^4)^2}\leq \dfrac{(x+y)^2}{4(xy)^2}=\underbrace{\dfrac{1}{4}\left(\dfrac{1}{y}+\dfrac{1}{x}\right)^2}_{g(x)}

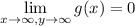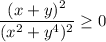
Очевидно, \lim\limits _{x\to\infty,y\to\infty}g(x)=0. При этом \dfrac{(x+y)^2}{(x^2+y^4)^2}\geq 0

Значит,

0\leq \lim\limits _{x\to\infty,y\to\infty}\dfrac{(x+y)^2}{(x^2+y^4)^2}\leq 0\Rightarrow \lim\limits _{x\to\infty,y\to\infty}\dfrac{(x+y)^2}{(x^2+y^4)^2}=0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
lenaseredenko lenaseredenko  18.05.2020 12:05
Даша прочитала 123 страницы, что составило 4/13 количества страниц в книге. Сколько всего страниц в книге?​...
малинка188 малинка188  18.05.2020 12:05
Кто я?аривдри овол ол лводатылота...
panerik6 panerik6  18.05.2020 12:05
4. Начертите тупой угол RQL, отметьте на его стороне QR точку A. Проведите через точку A прямую, перпендикулярную прямой QR, и прямую, перпендикулярную прямой...
LONNI34 LONNI34  18.05.2020 12:05
Автомобиль ехал 2 часа со скоростью 63,7 км/час и 3час со скоростью 71,8 км / год.Найты среднюю скорость. Пишите вон так 1)(...)-Тут обяснение обизательно 2)(...)-Тут обяснение...
1Max8 1Max8  18.05.2020 12:05
Яке з чисел є розв’язком нерівності (х-1)2(х-7) 0? А Б В Г 7 2 1 8...
inferatu777 inferatu777  18.05.2020 12:16
Үлкен текше неше кіші текшеден құралған​...
ZhanelTømmeraas ZhanelTømmeraas  18.05.2020 12:16
Даны координаты трех вершин прямоугольника ABCD: A(-2;-3),B(-2;5) и C(4;5). 1)начертите этот прямоугольник 2)найдите координаты вершины D 3)найдите координаты точки пересечения...
ХранительТьмы228 ХранительТьмы228  18.05.2020 12:19
Найдите значение выражения 2\5-3\4|x+1\3 при x=1,2...
tvoyamamka7 tvoyamamka7  18.05.2020 12:19
2) Какое количество оборотов сделает калесо велосипеда радиусом 0,7 м, на расстоянии 439,6 м.​...
Водород56 Водород56  18.05.2020 12:19
Номер 1061 а) и б Никак не могу разобраться с этими уравнениями. Заранее...

Популярные вопросы